13.3
Impact Factor
Theranostics 2016; 6(10):1651-1671. doi:10.7150/thno.15019 This issue Cite
Review
Standards and Methodologies for Characterizing Radiobiological Impact of High-Z Nanoparticles
Radiation Dosimetry, National Physical Laboratory, Hampton Road, Teddington, Middlesex, TW11 0LW, UK.
Received 2016-1-19; Accepted 2016-5-13; Published 2016-6-20
Abstract
Research on the application of high-Z nanoparticles (NPs) in cancer treatment and diagnosis has recently been the subject of growing interest, with much promise being shown with regards to a potential transition into clinical practice. In spite of numerous publications related to the development and application of nanoparticles for use with ionizing radiation, the literature is lacking coherent and systematic experimental approaches to fully evaluate the radiobiological effectiveness of NPs, validate mechanistic models and allow direct comparison of the studies undertaken by various research groups. The lack of standards and established methodology is commonly recognised as a major obstacle for the transition of innovative research ideas into clinical practice. This review provides a comprehensive overview of radiobiological techniques and quantification methods used in in vitro studies on high-Z nanoparticles and aims to provide recommendations for future standardization for NP-mediated radiation research.
Keywords: gold nanoparticle, clonogenic assay, reactive oxygen species, DNA damage, Monte Carlo.
Introduction
Ionizing radiation is widely used in medicine for both therapeutic and diagnostic purposes. In particular, radiotherapy is one of the main cancer treatment strategies used for more than 50% of all cancer patients (over 14 million in 2012) [1, 2], whilst X-ray based diagnostics account for >65% of all imaging modalities [3] with over 70 million CT scans performed in the US alone in 2007 [4, 5]. Despite the undisputed advantages, exposure to ionizing radiation is also associated with health consequences owing to the inevitable radiation dose delivered to healthy tissues. In the past two decades world-wide research efforts have been focused on developing strategies to optimize the efficacy of radiotherapy and improve the imaging contrast and diagnostic power of radio-diagnostics. Supported by early studies from the 1970s and 1980s [6-9], showing that X-ray contrast agents exhibit dose enhancing effects during a course of radiotherapy, use of high-Z materials represent a very promising option for both radio-sensitization of tumours in radiation treatment and contrast enhancement in diagnostics [10, 11]. Recent achievements in nanotechnology have made it possible to manufacture a wide range of nano-products, which can be used for driving forward innovative cancer treatments and diagnostic strategies. Particular interest has been focused on gold nanoparticles (Au-NPs) due to their high atomic number (and therefore contrast with soft tissues), small size, natural preference to accumulate in tumours, biocompatibility, low toxicity, relatively easy synthesis and capability to bind with functional moieties within biological target [12]. All these features made Au-NPs highly desirable in various applications, including imaging [13], targeted drug delivery [14] and radiotherapy [15]. Several studies have demonstrated in vitro and in vivo NP radiation enhancement effects [16, 17]. However, translation of such findings into clinical practice has been hampered by the fact that the exact mechanism of sensitisation is not yet fully understood. This poses a problem in terms of both accurate treatment planning for radiotherapy comparable with existing practice and evaluating the long-term radiation risks of using nanoparticle contrast agents. According to classical models, radiosensitisation has mainly been attributed to physical dose enhancement occurring at kilovoltage (kV) photon energies. This is due to strong photoelectric photon absorption by high-Z materials,with a subsequent cascade of low energy photoelectrons and Auger electrons [18]. However, these electrons have a very short (nm-µm) range in tissues and can deliver high doses in the NP immediate vicinity, [19] this alters the quality of the incident radiation, causing [20] complex patterns of ionization which ultimately results in lethal damage to cells. In parallel, there has been an increase in the number of reports indicating the impact of nanoparticles on cell cycle, metabolic activities and DNA repair pathways with consequent repercussion on the cellular radiation response. As such, the resulting overall radiobiological effects are likely to depend on a complex range of physical, chemical and biological parameters [21] such as nanoparticle size, material, charge, coating, reactive radical production, cellular uptake, turnover, cell cycle etc. Current models for the various physical, chemical and biological enhancements of radiation effects in the presence of NPs have been reviewed in detail by Her et al. [21]. Precise and accurate experiments are still required to generate high-quality and reproducible data to test these models and formulate new hypotheses. Such experiments will provide a more complete understanding of the mechanisms affecting the radiobiological response of tissue and cell systems treated with nanoparticles. In spite of numerous publications related to the use of NPs with radiation, the literature is lacking guidance on systematic and rigorous methodologies suitable to evaluate the effectiveness of NPs and/or directly compare the studies undertaken by different groups. This is particularly crucial when considering the large range of experimental systems and NP parameters available, such a range provides a great deal of complexity and difficulty in identifying ideal NP designs and formulations when attempting to optimise their clinical application [20]. Although the techniques used may be well established and commonly used assays, their adaptation to NP and radiation-related investigations and, moreover, the quantification of the NP induced effects is not always straightforward. Having a comprehensive list of procedures and clear directives on the quantification and comparison methods used to evaluate radiation enhancement owing to the application of NPs would help the nanoparticle and radiobiological community to gain a better understanding of NP-mediated effects and accelerate the translation of NP studies to the clinical stage. Moreover, the size, shape, clustering properties and surface chemistry of the nanoparticles play a critical role in bio-distribution, targeted binding and clearance of the nanoparticles from the body [22].
Previous reviews have focused on summarising NP data obtained as a function of different experimental conditions [23], clinical potentials of NP based strategies [24] or key parameters regulating radio-sensitization [21, 25] and highlighting the pathways to possible clinical implementation [20]. We reviewed 98 papers published between 2002 and 2015 on in vitro nanoparticle studies with ionizing radiation to report the approaches used to assess and quantify the radiobiological impact of high-Z NPs. A wide range of assays and quantification methods have been used, often with confusing terminology, and not always in line with available international recommendations. The lack of standardization is partially responsible for the slow transition of NP strategies to clinical applications. This review therefore aims to highlight potentials and shortcomings of the methodology used and it is expected to contribute to the standardization of pre-clinical radiobiological studies with NPs.
Measurement of NP radiation-enhancement effect
Cell survival
The most widely used technique in radiobiology to study the effectiveness of a treatment is the clonogenic (or colony formation) assay which was first developed almost 60 years ago by Puck and Markus [26]. This in vitro technique allows assessment of the cytotoxicity of radiation by testing the ability of a single cell to grow into a colony, i.e. to undergo continuous proliferation. The cell is considered radio-biologically dead if it has lost its reproductive viability to produce progeny [27]. This type of assay has developed into the most extensively used technique for evaluating the radiation sensitivity of different cell lines and it is considered the “gold standard” for radiation response. Conventionally, the outcomes of colony formation assays are presented as so-called survival curves representing the survival fraction (SF), i.e. the number of colonies that are formed after treatment, as a function of radiation dose (D) [28]. Alternative methods for estimating the survival fraction have been developed using cell viability tests such as the methyl-thiazol-tetrazolium (MTT) assay and the trypan blue exclusion test. Validation and limitation of such methods for radiobiological applications have been extensively discussed [29, 30] in the literature and the same arguments as for the colony formation assay apply for NP investigations.
The experimental curve of the survival data is generally fitted with a linear-quadratic (LQ) model, which is given by:
(1)
where SF is the fraction of surviving cells, α and β are linear and quadratic parameters of the model, respectively and D is the radiation dose delivered. Although the linear-quadratic model is currently the most widely used model to describe the cell survival curve, it must be pointed out that alternative models are also employed [31]. Detailed discussion on the theoretical and experimental models used to describe the survival curves is beyond the scope of this review, but where necessary, reference to specific models will be made to discuss the quantification methods adopted.
Approaches to quantify NP radiation enhancement effects from clonogenic survival data
In order to provide a comprehensive understanding of the dose-response relationship resulting from a modifier (such as the application of NPs to biological systems) it is necessary to gather a full set of dose response data for the reference and the modified systems. According to ICRU Report 30 [32], when clonogenic survival data are available and the two curves are not directly proportional, the entire curve needs to be taken into account in order to quantify the effect of the modifier.
Enhancement quantification in terms of mean inactivation dose (MID)
The use of the Mean Inactivation Dose (MID) offers a possible method for quantifying the differences between survival curves through a single parameter whilst taking into account the whole survival curve. The concept of MID was first introduced by Kellerer and Hug [33]. The authors proposed that the survival fraction as a function of dose, SF(D), can be considered as an integral probability distribution. SF(D) would therefore represent the probability that a dose larger than D is necessary to inactivate a cell which has been randomly selected from the population. Mathematically, MID is calculated simply by estimating the area under the survival curve [34]:
MID =(2)
Adoption of the MID concept has several advantages: (i) it is representative for the whole cell population; (ii) it minimizes the fluctuations in the survival curves and (iii) it takes into account the whole survival curve. Therefore, MID appears to be a useful concept for specifying intrinsic radio-sensitivity of biological cell systems [35] and is endorsed by ICRU Report 30 [32].
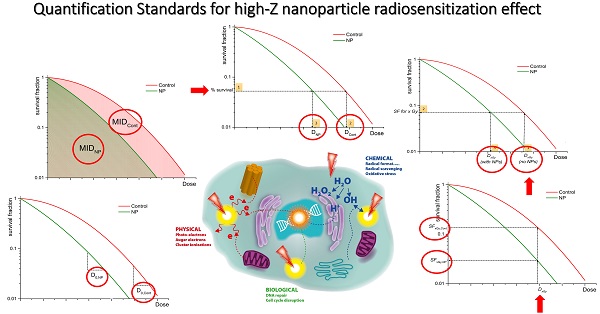
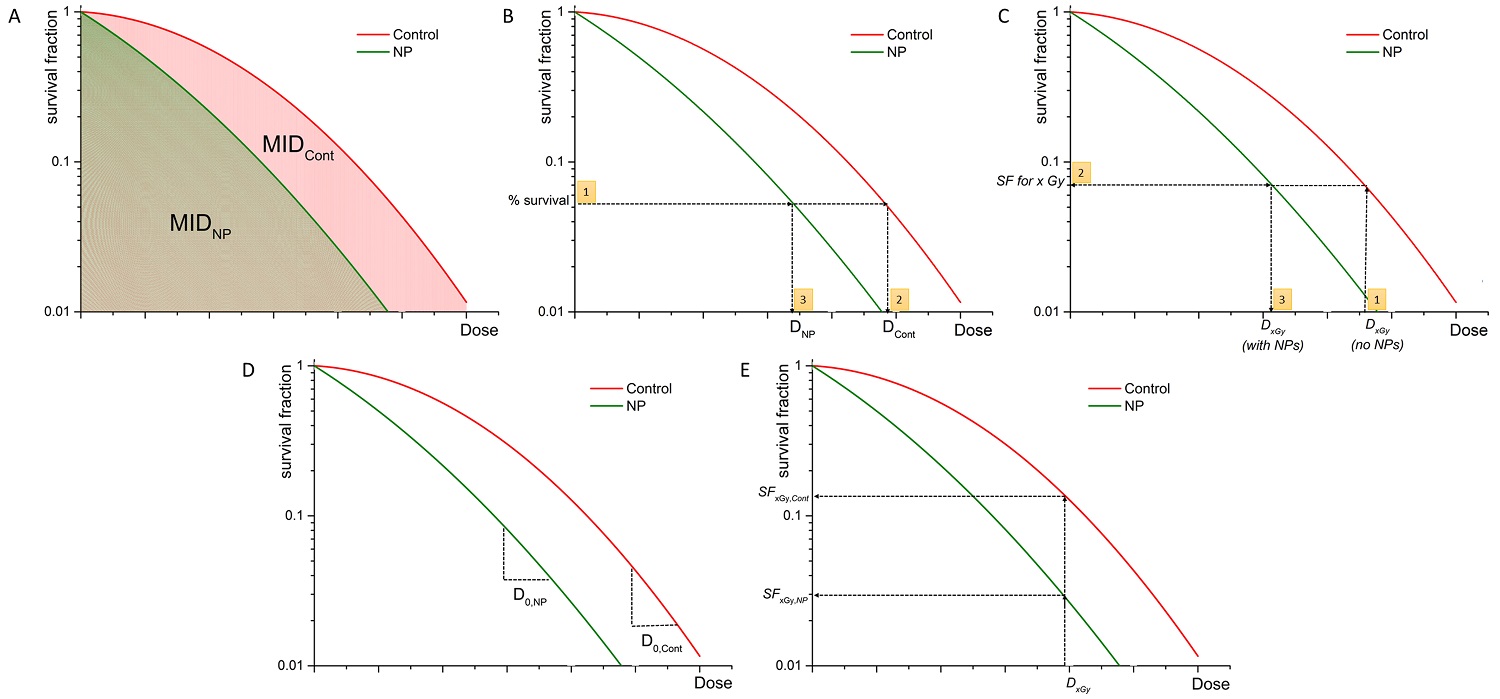
As a result, several authors quantified the radiobiological impact of NPs by calculating the ratio of MIDs of non-exposed cells with nanoparticle exposed cells [16, 36-40] and called this quantity sensitizer enhancement ratio (Figure 1A) for a given nanoparticle concentration (SERNP).
(3)
where the subscripts Cont and NP refer to nanoparticle and control (i.e. radiation alone) survival curves, respectively.
Both Jain et al. [16] and McMahon et al. [37] investigated radiosensitizing effects of Au-NPs for 6 and 15 MV photon irradiations and used the MID concept to quantify the effect. In both studies, the linear-quadratic model was used to fit the experimental data and calculate MIDs and SER. When adopting the LQ model for fitting the experimental data the SER can be expressed in an analytical form by solving the integrals (given by equation (2)) as
(4)
Enhancement quantification in terms of alpha and beta parameters
More generally, the linear (α) and quadratic (β) parameters from the LQ model could be used to characterize the nanoparticle enhancement effect. Although these parameters are usually reported in the majority of the NP radiobiological studies [36, 41-44] not all of them discuss qualitatively or quantitatively the difference in α and β for irradiations with and without NPs. McMahon et al. [44] have identified significant increases in α (and little or no change in β) as a function of NP concentration, unlike Jain et al. [16], where an increase in both α and β components of the LQ curve was observed for an increase of NP concentration. Although the LQ model is phenomenological, the alpha parameter is generally associated with the formation of complex lethal DNA damage whilst the beta parameter indicates sub-lethal lesions. Conclusions from the changes in biological effectiveness and the mechanisms underpinning it could therefore be drawn from analysing the variation in the alpha and beta parameters for the control and the NP related survival curves. This is particularly the case if the role of NP concentration and cellular uptake is to be addressed.
Graphical representation of quantification of NP-mediated radiation enhancement effect from clonogenic survival data using: (a) SERNP=MIDCont/MIDNP; (b) DMRx%= DCont/DNP at x% effect is calculated as follows: (1) % survival is selected, (2) dose DCont is evaluated, (3) dose DNP is evaluated for the same % survival; (c) DEFx = Dx,Gy (no NPs) / Dx,Gy (with NPs) is calculated through estimation of the SF level through the following steps: (1) Dx Gy (no NP) is chosen, (2) SF at Dx,Gy (no NP) is evaluated, (3) Dx,Gy (with NPs) is calculated); (d) REF = D0,NP / D0,Cont; (e) RERxGy = SFxGy,Cont / SFxGy,NP.
Finally, the α/β ratio is a widely used parameter in radiotherapy to indicate the intrinsic radio-sensitivity of samples. On the assumption that NPs interfere with the cellular repair processes, evaluation of the change of the α/β parameter would be useful for quantifying the radiobiological impact of specific NPs. Change in the α/β ratio would indicate any radio-sensitivity changes of the system as being induced by the NPs. Currently, this approach has not been adopted by any investigation.
Enhancement quantification in terms of Dose Modifying Ratio (DMRx%)
The ICRU Report 30 also suggests the Dose Modification Ratio (DMR) as a parameter to quantify differences between survival curves (Figure 1B). This is defined as the ratio of the dose under reference conditions to produce the same effect (x%):
(5)
It is essential to note that the DMR may be dependent on the effect and it would still require a full set of survival data and use of a cell survival model to fit the experimental data. Although DMR offers a conceptual straightforward link between biological effect and dose absorbed, the same effect might be produced by different mechanisms despite significant differences in the overall survival curves. As cell survival is the end result of a complex sequence of biological and chemical changes, it is recommended to report the DMR at more than one survival level together with all the other factors that may modify dose dependence for the reference and test conditions [32], in order to provide an effective quantification of the radiation response changes. When two dose responses are related by a constant factor on the dose scale, dose modification ratios are independent of the effect and the DMR is then specified as dose modification factor (DMF).
The DMR concept has been commonly used in the reviewed literature [17, 41, 42, 45-50]. However, there are vast discrepancies in the terminology, the effect adopted and the calculation methods. For instance, Kaur et al. [50] and Chithrani et al. [17] calculated DMR at 90% and 10% level, respectively, and called it radiosensitivity enhancement factor (REF) whilst Jeynes et al. [47] used the 50% level and named it sensitizer enhancement ratio (SER) and Chattopadhyay et al. [46] adopted the 10% level but referred to it as dose enhancement ratio (DER). In all cases, the LQ model was used. Please note that the terminology used in literature is not consistent and various groups use the same terms to describe NP-mediated effects which are actually defined in different ways.
The choice of survival level for the DMR calculation is arbitrary and it is usually between 10% and 90% as these usually represent situations of practical interest where either small or large effects of radiation are expected. From a statistical point of view, considering that uncertainties for measurements of small levels of survival (large number of cells are usually used for these measurements) are usually smaller than for higher survival levels, the overall uncertainties related to DMR10% are expected to be smaller than those for DMR90%. It must be noted that the vast majority of the studies only report DMR for a single survival level.
DMR at the 2 Gy survival level (SF2)
Previous studies [51, 52] have shown that the initial slope of the survival curve (rather than the final slope) correlates well with clinical outcomes. This initial region of the survival curve is considered to be best characterized by the survival level at a dose of 2 Gy, known as SF2. 2 Gy represents also the typical individual dose of conventional radiotherapy fractionation delivery. Therefore, some authors [43, 53] investigating efficacy of nanoparticles in in vitro have used this quantity to estimate the survival level at which to calculate the DMR. Although less common, using such an approach, a Dose Enhancement Factor (DEF) (Figure 1C) has been defined as the ratio of doses which lead to the same levels of cell survival as a particular dose delivered to the control sample (e.g. 2 Gy).
DEFxGy = dose of x Gy (no NP)/dose required to produce in test samples (with NP) the same SF as in control with x Gy (6)
Although the majority of studies calculating DEF have used the 2 Gy dose, some investigations have used the level of cells surviving an acute dose of 3 Gy (SF3) [54-56], 4 Gy (SF4) [36, 56, 57] and 8 Gy (SF8) [56, 57]. None of the authors justified their choice of the selected dose level for calculation of the dose enhancement factor. However, Taggart with her colleagues [56] presented a set of DEFs for various dose levels warning about the wide range of obtainable results. The DEF so defined is essentially a special case of the DMR in which the effect level is not arbitrarily chosen but calculated for the control samples for a dose of specific interest. The main advantage of this approach is represented by the selection of a specific dose of interest to evaluate the effect of NPs in well-defined scenarios. This approach therefore deals exclusively with physical quantities making the analysis applicable to all those cases where there is no natural selection of the effect level which may involve complex procedures or even some subjectivity. On the other hand, studies reporting DEF at various survival levels clearly show the strong dependency on the dose levels, advocating the use of multiple doses to provide a more comprehensive picture of the radiobiological effect of nanoparticles.
Radiation enhancement factor (REF) using the multi-target model
An alternative method for quantifying the radiobiological effect of NPs is offered by the adoption of the multi-target model, which was developed in the attempt to precisely address the straight portion of the high dose region of the survival curve and is given by the following relation:
(7)
This model describes the slope of the survival curve by D0 (the dose to reduce cell survival to 37% of its value at any point on the final near exponential part of the curve) and the extrapolation number n (a measure of the width of the shoulder). Using the multi-target single hit (n=1) model, Cui et al. [58] defined the radiosensitivity enhancement factor (REF) (Figure 1D) as the ratio of the D0 parameters for the NP and control exposures:
(8)
Interestingly, in the evaluation of such radiation enhancement factor, the parameter related to the reference radiation appears at the denominator, contrary to DMR and the previously discussed methods. The main advantage of the REF appears to be in the evaluation of the NP effect for high dose levels, with the multi-target model providing a better description of experimental data compared to the linear-quadratic model. To date, such approach has only been adopted by Cui et al. [58].
Radiation enhancement ratio (RER)
For historical reasons and for the lack of a unified common effect scale to characterize radiation effects, virtually all radiobiological concepts have been defined on an iso-effect basis using the ratio of doses (well defined for all radiation types) rather than on an iso-dose basis which would require the ratio of the effects. Despite this, many authors have found it useful to characterize the radiobiological effect of NPs by comparing the different levels of effects following a given radiation dose. The Radiation Enhancement Ratio (RERxGy) (Figure 1E) has therefore been defined as the ratio of survival fractions without and with NPs for a specific dose:
(9)
Although this parameter so defined is limited to cell survival studies, it has the benefit of directly portraying the amount of variation of the biological response caused by the NPs at a specific dose level. Such approach requires an accurate determination of the dose absorbed in the presence of NPs and assumes no change in the radiation quality. For the same considerations mentioned for the DMRx%, RERxGy at multiple dose levels should be reported for a comprehensive evaluation of the effect of NPs. RERxGy has been reported in literature either as sensitizer enhancement ratio (SER) or dose enhancement factor (DEF) [54, 55, 59-61].
The overview of up-to-date NP-mediated enhancement factors used in literature in clonogenic studies is given in Table 1.
Cellular radiation response strongly depends on the cell cycle stage in which the cells are exposed and their ability to repair the initial radiation damage through complex DNA repair and metabolic pathways. Owing to their size and chemical composition, NPs can be considered as chemical agents altering the cellular functions including progression through the cell cycle an effect which has been reported in several studies [66-69]. Despite this, only a minority of radiobiological studies [16, 70, 71] have included changes in the cell cycle due to NPs in their quantification of the radio-sensitization as well as investigations of the underpinning mechanisms, as indicated in Table 2. The methodology for assessing and quantifying the distribution of a cell population through the cell cycle is well established and it is mainly centred on flow cytometry analysis. As such measurements are not specific for radiobiology or NP studies, they will not be covered in this manuscript, but the reader is encouraged to refer to the work of Wilson [72] for technical details.
Overview of modification enhancement ratios used in nanoparticle studies.
| Cell line | Radiation source | NP material (size) | Enhancement factor used | Reference |
|---|---|---|---|---|
| GES-1 BGC823 SGC7901 MKN45 | 4 MeV electrons | DOC-NP (85 nm) | REF = D0,NP / D0,Cont multi-target single hit model (but referred to as SER) | [58] |
| MDA-MB-231 DU-145 T98G | 225 kVp X-rays | Au-NP (1.9 nm) | DEF2Gy DEF4Gy DEF8Gy | [56] |
| DU-145 MDA-231-B MCF-7 L-132 T98G AGO-1522B | 160 kVp X-rays | Au-NP (1.9 nm) | DEF2Gy | [62] |
| HeLa | Co-60 | Au-NP (50 nm) | RER2Gy (but referred to as DEF2Gy) | [59] |
| HeLa | 105 kVp X-rays 220 kVp X-rays Cs-137 6 MV X-rays | Au-NP (14, 50,74 nm) | DMR10% (but referred to as REF) | [17] |
| RT112 | 250 kVp X-rays 3 MeV protons | Au-NP (50 nm) | DMR50% (but referred to as SER) | [47] |
| MDA-MB-23 | 160 kVp X-rays | Au-NP (1.9 nm) | α, β - qualitative analysis | [44] |
| MDA-MB-23 | 225 kVp X-rays | Au-NP (2.7 nm) | DMR10% (but referred to as DEF) α, β - qualitative analysis | [41] |
| MDA-MB-23 DU145 | 160 kVp X-rays | Au-NP (1.9 nm) | SER α, β - qualitative analysis | [36] |
| DU145 MDA-MB-23 L132 | 160 kVp X-rays 6 MV X-rays 15 MV X-rays | Au-NP (1.9 nm) | SER α, β - qualitative analysis SF4 | [16] |
| MDA-MB-23 | 6 MV X-rays 15 MV X-rays | Au-NP (1.9 nm) | SER | [37] |
| DU145 MDA-MB-23 L132 | 160 kVp X-rays | Au-NP (1.9 nm) | RER3Gy (but referred to as SER) | [54] |
| BAECs | 80 kVp X-rays 150 kVp Xrays 6 MeV 12 MeV | Au-NP (1.9 nm) | DMR90% (but referred to as DEF) | [49] |
| CT26 | synchrotoron X-ray 6 MeV electrons | Au-NP (2 nm) | SF3 | [55] |
| F98 | 50 keV synchrotoron X-ray | Au-NP (1.9, 15 nm) | DMR10% (but referred to as SER10%) | [45] |
| MDA-MB-361 | 100 kVp X-rays | Au-NP | DMR10% (but referred to as DEF) | [46] |
| HeLa | Co-60 62 MeV carbon ions | Glu-Au-NP (4 - 14 nm) | DMR90% (but referred to as REF) | [50] |
| SNB-19 U87MG | MeV photons (LINAC) | Ti-NP (10 nm) | SF2 α, β - qualitative analysis | [43] |
| BAOEC | 30-100 keV synchrotron X-rays | Au-NP (1.9 nm) | DMR90% (but referred to as DEF) α, β - qualitative analysis | [42] |
| HeLa | Cs-137 | PEG-Au-NP (4.8 - 47 nm) | DMR50% (but referred to as REF) | [48] |
| A549 | 6 MV X-rays | Glu-Au-NP (13 nm) | SER | [38] |
| HT1080 | Co-60 6 MV X-rays | NBTXR3-NP (50 nm) | DEF4Gy DEF8Gy | [57] |
| GBM | 150 kVp X-rays | Au-NP (12 nm) | RER4Gy (but referred to as SER) | [60] |
| U87 | Cs-137 | Gd2O3-NP (sub-10 nm) | SF2 SF5 SF8 | [63] |
| Panc1 | 220 kVp 6 MV X-rays | AGuIX-NP | SER (but referred to as DEF) DMR20% (but referred to as DEF20%) RER4Gy (but referred to as SER4Gy) | [61] |
| U87 | Cs-137 | BSA-Au-NP (18 nm) | DEF2Gy (but referred to as SER2Gy) | [64] |
| MDA-MB-231 | 6 MV | Glu-Au-NP (16 nm) | SER | [40] |
| PC3 | 6 MV | PEG-Au-NP (~30 mm) | DMR20% (but referred to as REF) | [65] |
Methods used in the literature for assessment of NP uptake, intracellular distribution and cell cycle.
| Ref. | NP uptake assessment | Quantification of uptake | Intracellular distribution/localization | Cell cycle assessment |
|---|---|---|---|---|
| [73] | ICP-AES | pg/cell | TEM | Flow cytometry |
| [65] | ICP-MS | Relative concentration of internalized gold | TEM | n/a |
| [41] | ICP-AES | pg/cell | TEM | n/a |
| [36] | ICP-AES | # of NP/cell | TEM | n/a |
| [63] | ICP-OES | pg/cell | TEM | n/a |
| [37] | ICP-AES | # of NP/cell | TEM | Flow cytometry |
| [82] | n/a | n/a | TEM | n/a |
| [79] | ICP analysis | # of NP/cell | TEM | n/a |
| [71] | ICP-MS | # of NP/cell | n/a | Flow cytometry |
| [83] | n/a | n/a | TEM | n/a |
| [80] | ICP-MS | # of NP/cell | TEM | n/a |
| [84] | n/a | n/a | TEM | n/a |
| [48] | n/a | n/a | TEM | n/a |
| [50] | n/a | n/a | TEM | n/a |
| [59] | ICP-AES | # of NP/cell | n/a | n/a |
| [81] | ICP-AES | # of NP/cell | n/a | Flow cytometry |
Uptake and intracellular localization of high-Z nanoparticles
A critical step in high-Z NP radiobiological studies includes quantifying the number of nanoparticles (or amount of material) taken up by cells and tissues. The importance of which has been highlighted by several publications [37, 41, 73, 74] showing how various cell lines exhibit different assimilation properties both in terms of total amount of NPs and rate. Considering the underlying mechanisms responsible for the NP-mediated radiation effect enhancement, as discussed below in the reactive radical and Monte Carlo sections, it is likely that the differences in the radiation effect enhancement reported between studied cell lines are down to different concentrations and localization of NPs present in the cells at the time of irradiation. Inductively coupled plasma (ICP) techniques coupled either with atomic emission spectroscopy (ICP-AES) or mass spectrometry (ICP-MS) are currently the “gold standard” in measuring the amount of nanoparticles residing in cells [75-77]. It has been demonstrated that combining ICP sources with MS or AES provides high sensitivity and a robust tool for elemental analysis and it is widely used. OES-optical emission spectroscopy and AES-atomic emission spectroscopy effectively represent the same method and technology used for elemental analysis and these names are used in literature interchangeably. The ICP techniques use electromagnetic induction to produce an argon plasma whose temperature can range from 6000 K to 10 000 K, which is enough to break most molecular and ionic bonds of the sample. For ICP-AES, the sample atoms are excited in the plasma chamber and a spectrometer is used to resolve and quantify the electromagnetic radiation emitted by the various ions. In the ICP-MS, the sample is atomized and ionized in the plasma chamber and the mass-to-charge ratio is obtained for each ion using a mass spectrometer. Although both methods (i.e., ICP-MS and ICP-AES) are well-suited to determine the concentration of nanoparticles, ICP-MS is about three orders of magnitude more sensitive than ICP-AES. The accuracy of the ICP-MS and ICP-AES analysis is 0.5-3% and 3-5% relative to the reported value, respectively [78]. Several authors have used these techniques for NP studies expressing either the number of nanoparticles per cell [36, 37, 59, 71, 79-81] or the amount of material per cell [41, 63, 73] (see Table 2). Although it is straightforward to convert the material mass into number of NPs, this requires accurate information about the size and elemental composition of the NPs and assumes a uniform distribution.
Several groups [74, 85, 86] have also taken a step further and carried out theoretical (Monte Carlo and analytical) investigations in the attempt to correlate radiation effect enhancement with intracellular localization of high-Z nanoparticles. These studies provided useful insight into choice of nanoparticle material, size, and sub-cellular targeting location in order to achieve maximum efficacy in NP-enhanced radiation dose and demonstrated that the distribution of NPs within cells plays a paramount role in radio-sensitization. It is, therefore, important to address this aspect experimentally and develop methods for quantifying NPs in sub-cellular organelles. Microscopic methods are the most commonly used techniques to identify the subcellular location of nanoparticles. Optical microscopy, however, does not provide sufficient resolution due to the inherent limits of this technique and the majority of studies have employed transmission electron microscopy (TEM) (Table 2). It must be noted that this method has been used to provide solely qualitative information as only a limited number of images are usually collected and analysed. In order to provide statistically relevant quantification with TEM a large, randomly chosen, number of images should be recorded and analysed.
Production of reactive oxygen species
The biological effects of radiation result principally from damage to the cell's DNA damage which (in mammalian cells) arises from either direct or indirect effects. When ionising radiation is absorbed in biological material, there is a possibility that it will interact directly with the DNA in the cells. The atoms of this target itself may be ionized or excited (direct action), initiating the chain of events that leads to a biological change. However, as the majority of the ionization events occur in water molecules, the indirect action of radiation mediated mainly by reactive oxygen species (ROS) is the leading effect of DNA damage, [87] especially for low LET radiation [47, 88]. ROS is a collective term for different reactive molecules and free radicals derived from molecular oxygen. The most common ROS include hydroxyl radicals (•OH) (which contribute to 60% - 90% of all DNA lesions [89]), singlet oxygen (1O2), superoxide anions (O2-) and hydrogen peroxide (H2O2), all of which are more reactive than oxygen (O2) itself.
It has been demonstrated that metal salts and metal ions, such as certain NPs with reactive sites on their surfaces, can induce oxidative stress through generation of ROS [90-94]. On the other hand, some nanoparticle coatings, such as derivatives of thiols or citric acids, are well-known hydroxyl radical scavengers [95, 96] which can contribute to maintain an optimum physiological level of ROS in the cells. Moreover, the NPs may interact directly with the incoming ionizing radiation or any of the intermediate chemical products to alter the final spectrum and yield of ROS. Initial models of NP-mediated effects of dose enhancement in cells accounted only for the physical dose increase and, more recently, the localised effect of a cascade of Auger electrons. The mechanisms for ROS generation may be different for each NP type and to date the exact underlying cellular mechanism for ROS generation is not fully understood. A thorough understanding of the ROS production associated with NPs is critical in order to address the mechanism underpinning the biological response, as is an adequate methodology to accurately and reliably measure the yield and spectrum of ROS.
There are several techniques that can be employed to evaluate the level of ROS. The most common tests are colorimetric methods and fluorescent or chemiluminescent dyes (e.g., 2',7'-dichlorodihydrofluorescein-diacetate (H2DCF-DA)). J.F. Woolley et al. [97] provided a table detailing the different aspects of the 'ideal' fluorescent ROS detecting probe. This includes vital properties such as membrane permeability, bio-orthogonality and non-toxicity of the probe, signal-to-noise ratio and an effective chemo-selectivity in order to avoid cross-reactivity and ambiguity of the type of ROS involved in the reaction. One of the difficulties with the reaction rate involving these fluorescent probes, is that the dyes are in competition with the various antioxidant enzymes in the cell. Therefore, the quantitative information gleaned from studies utilizing fluorescent probes should be carefully analysed, taking into account this confounding factor. More information on current advances in ROS detection are available in the literature [97]. This review will focus on the quantification of the changes caused by the presence of NP in the irradiated samples.
In-cell fluorescent assays
Measurement of hydroxyl, peroxyl and other ROS activity in cells is generally performed with fluorogenic or chemiluminogenic substances, which serve as hydrogen donors. Several probes have been investigated and used for in-sample measurements of ROS and/or oxidative stress following exposure to ionizing radiation [97]. The most extensively used are DCFH and H2DCF [98-100], which have also been employed for NP studies [101]; these compounds are usually applied through the cell culture medium and rapidly taken up by the cell. Oxidation of the compound molecules by ROS converts the probe molecules to a fluorescent product with high fluorescence quantum yield that can be easily monitored by several fluorescence-based techniques, including confocal microscopy and flow cytometry. Such assays can provide an assessment of level of oxidative stress by evaluating the relative yield of ROS for the studied in vitro system compared to its control. However this technique does not provide an absolute quantitative measurement of ROS.
With respect to NP studies, Pujalte et al. [94] reported the change in the ROS yield in terms of % of control by evaluating the ratio of the fluorescence signals (measured as peak fluorescence for the specific excitation and emission wavelength of the dye used acquired through a fluorimeter) from the NP treated and control samples following exposure to known doses of radiation. On the other hand, Klein et al. [102, 103] evaluated the relative fluorescence intensity by integrating the whole emission spectra acquired on a spectro-fluorimeter. The fluorescence intensity values of different NP exposures were then related to those obtained from fluorescence measurements of cells in the pure culture medium and specified as % increase of fluorescence. Furthermore, Geng et al. [81] detected fluorescence intensity under confocal microscopy and analysed the images by plotting 3D surface plots of the fluorescence and calculating the peak volume intensities and the cellular cross-sections. The mean increase in fluorescence intensity was defined as a peak volume of the fluorescence divided by the cell cross-section area and normalized to the control images.
It must be noted that in order to assess the change in radiation induced ROS yield caused by the presence of NPs, multiple controls are usually required. The intensity from irradiated samples treated with NPs will have to be compared to NP-treated but non-irradiated samples and related to the intensity variation for irradiated versus non-irradiated samples (i.e. changes due to irradiation alone). Relative changes in the ROS production should therefore be quantified as fluorescence intensity ratio (FIR):
(10)
where INP+Irr refers to the intensity of irradiated samples treated with NPs, INP is the intensity of non-irradiated samples treated with NPs, IIrr and ICont is the intensity for non-NP treated irradiated and control samples, respectively. As shown in Table 3, the main discrepancy between the ROS measurements with NPs using fluorescence assays is related to the fluorescence measurement itself. Depending on the aim of the study, the effect of NPs is generally evaluated through the ratio of the intensities, making this approach suitable for relative measurements (under appropriate experimental conditions) but with severe limitations with regard to absolute change in ROS and comparison of different NP products and experimental conditions.
Overview of ROS fluorescence measurement in NP studies.
| Probe | Intensity measurement method | NP effect quantification method | Reference |
|---|---|---|---|
| APF (λex = 490 nm, λem = 515 nm) for detection of ‑OH radical. DHE (λex = 465 nm, λex =585 nm) for detection of singlet oxygen (1O2). | Microplate reader | INP+Ir / IIrr | [114] |
| DCF-DA (λex = 518 nm, λem = 605 nm) | Flow cytometry | INP+Irr / IControl | [62] |
| DCF-DA (λex = 480 nm, λem = 520 nm) | Fluorimeter | INP+Irr / IControl using a bespoke control solution | [94] |
| DCF-DA (λex = 480 nm, λem = 500-700 nm) | Spectrofluorometer | INP+Irr / IControl | [102] |
| DCF-DA (λex = 480 nm, λem = 500-700 nm) | Confocal microscope | INP+Irr / IControl | [81] |
| DCF-DA Wavelength not specified | Not stated | Qualitative comparison of INP+Irr and INP | [88] |
| DCF-DA Wavelength not specified | Flow cytometry | INP+Irr / IIrr | [54] |
| DCF-DA Wavelength not specified | Flow cytometry | INP+Irr / IControl INP / IControl IIrr / IControl | [58] |
| DCF-DA (λex = 480 nm, λem = 500-700 nm) | Spectrofluorometer | INP+Irr / IControl | [103] |
| DCF-DA (λex = 492-495 nm, λem = 517-527 nm) | Microplate reader | INP+Irr / IControl INP+Irr / IIrr | [115] |
Susceptibility of in-cell ROS assays
Assays for measuring ROS possess certain weaknesses, particularly a susceptibility to numerous artefacts resulting from sample preparation or from the analytical method itself. Organic solvents which are used to dissolve the test compounds, such as dimethyl sulfoxide (DMSO) or ethanol bring difficulties that all tests have in common. Namely, DMSO and ethanol are powerful hydroxyl scavengers [47, 104], which could lead to an underestimation of the amount of ROS produced. Additionally, it is vital to evaluate the impact of the test compounds as the results can be altered by changes in intermediate reactions taking place in the culture media that may lead to under- or overestimation of oxidative stress [99]. Another problem in ROS measurement through fluorescence techniques is the loss of signal, correlated with the photobleaching effect [105, 106]. The photobleaching effect plays a less significant role in relative quantification of ROS production, when the oxidative stress is expressed as a ratio of the effect in the studied and control system, therefore the effect itself cancels out. Additionally, fluorescence techniques can suffer from problems associated with detection technique itself such as non-linear response of the sensor (e.g. microscope cameras). The detailed description of the factors affecting quantitative accuracy of fluorescent measurements is outside the scope of this review but interested readers can find more information elsewhere [107-110].
There are several other practical drawbacks related to ROS quantification in the presence of NPs. First of all, the assumption that NPs do not change the chemical behaviour of a probe might not be correct as interactions among NPs and colorimetric and fluorescent dyes have been shown to lead to inaccurate absorbance and fluorescence measurements [111]. It is also well-known that various probes have affinity to specific oxygen species [112]. However, very few chemical probes are highly specific to a particular ROS, i.e. most of the probes interact with a range of radicals, and therefore the presence of NPs can alter the yield and spectrum of ROS while the probe response remains unchanged. Additionally, it is important to note that the chemical probe needs to be taken up by the cells, therefore it is necessary to establish whether NPs interfere with the probe uptake prior to carrying out experiments. As a result ROS measurements employing chemical probes need to be applied with a particular care and are not likely to be used in a quantitative manner. More details on ROS sensors focusing on nanoparticle applications can be found here [113].
Coumarin assay
Coumarin-3-carboxylic acid is a non-fluorescent organic chemical compound (C10H6O4) which upon interaction with OH radicals (as generated through radiation exposure) converts to 7-hydroxyl coumarin-3-carboxylic acid (among other products) which is a highly fluorescent substance. The interaction of coumarin with the hydroxyl radicals is a single step process which does not require additional catalysts. The intensity of the fluorescent irradiated solution is proportional to the number of hydroxyl coumarin molecules which is related to the yield of OH produced and therefore the dose delivered. Coumarin has already been suggested as a possible dosimeter in both bulk solutions and biological samples, indeed a few studies have characterized its performance as a function of common radiation parameters [116-118]. The coumarin has a high selectivity for OH radicals, its sensitivity and dose linearity across a wide range and moreover its compatibility with NPs (it does not induce aggregation) make it an ideal probe for assessment of the impact of NP on the radiation induced OH yield.
Quantification of OH produced in the presence or absence of NPs is possible through the use of a G-value, i.e. the number of moles of OH radicals produced per joule of radiation energy deposited in the sample solution. This approach allowed quantification of the OH production from irradiated samples containing NPs and thereby enabling comparison across different studies and validation of models.
The protocols [73, 119, 120] involve absolute calibration through use of a pure fluorescence coumarin product (7OH-coumarin) and estimation of the change in the coumarin-OH regioselectivity owing to the different type and concentration of NPs. Sicard-Roselli et al. [119] estimate this change in the coumarin response by back extrapolation through different concentrations of NPs. It is also important to take into account the possible quenching of the coumarin signal by the presence of NPs. When possible [73], this can be accomplished by simply removing the nanoparticles from the coumarin solution through centrifugation just before the readout stage. As an alternative approach, Sicard-Roselli et al. [119] used gold nanoparticles (32.5 nm diameter) synthetized by reduction through the tri-sodium citrate method. Such nanoparticles can be removed from the coumarin solution by inducing aggregation and precipitation through 1% (w/v) NaCl. Removal of NPs through centrifugation or NaCl is, however, not always feasible or practical (depending on the NPs coating and size) and alternative strategies might be necessary for using such methods for a wider range of NPs. These methods potentially include estimation of the coumarin quenching factor by NPs and consequent correction of the readout signal.
Use of the coumarin assay has highlighted the significant impact that NPs can have on the OH production, and when used in combination with cellular experiments [73] can be a powerful method to investigate the mechanisms for NP radiosensitization. According to Cheng et al. [121], the OH reaction yield can be enhanced by more than 3 orders of magnitude although this strongly depends on the chemical properties of the NPs and their functionalization shells [120]. Interestingly, using the coumarin method, Sicard-Roselli et al. [119] postulated three separate pathways for the production of OH radicals by ionizing radiation in the presence of NPs. This represents a development from previous models that only consider interaction of primary and secondary radiation from NPs with water molecules, but neglect the catalysis-like mechanism at the water-nanoparticle interface.
DNA damage
DNA is constantly subjected to damaging agents. DNA damage has been identified as a key element regulating radiation response. The impact of nanoparticle-mediated DNA damage needs to be addressed in quantitative and mechanistic studies. Several authors have compared the radiation-induced DNA damage in the presence or absence of nanoparticles. A number of strategies such as differential plasmid DNA migration on agarose gel electrophoresis, comet assay and immunostaining for γ-H2AX and 53BP1 foci have been reported to detect DNA damage. However, not much work has been done in order to establish quantities defining nanoparticle enhancement employing DNA damage assays.
Comet assay
The term 'comet assay' (single-cell gel electrophoresis) was first given by Olive et al. [122]. These assays provide information on the alteration of DNA following cell irradiation and are based on quantification of the denatured DNA fragments migrating out of the cell nucleus during electrophoresis. Several different attempts have been made to evaluate and quantify comet formation patterns, and a variety of commercial and freeware computer programs are available for assessing the resultant images. Most commonly, the distance of DNA migration from the body of the nuclear core is used to measure the extent of DNA damage when dealing with relatively low damage levels. However, this technique is not very useful in situations where DNA damage is relatively high, as with increasing extent of DNA damage the tail increases in intensity but not in length. The most accredited scoring method for comet evaluation is referred to as 'tail moment'. The concept of tail moment (calculated as tail length) as a measure of DNA migration was introduced by Olive et al. [123] and incorporates relative measurements of both the smallest detectable size of migrating DNA (reflected by the length of the comet tail) and the number of broken pieces of DNA (represented by the staining intensity of DNA in the tail). A tail moment, which is related to the number of DNA damages, is defined as the product of the percentage of DNA in the tail by the displacement between the head and the tail of the comet [124].
Miladi et al. [125], investigated the radiosensitizing effect of gold nanoparticles coated with gadolinium (Au@DTDTPA and Au@DTDTPA-Gd) which have been incorporated into the U87 cell line through single-cell gel electrophoresis comet assays. The group demonstrated a significant increase in the mean tail moment for cells incubated with Au-NPs with escalating dose. The mean tail moments of samples were compared to those of the control groups (i.e. irradiated cells without incubation in nanoparticles and non-irradiated cells only incubated with NPs). Using a similar protocol, Mowat et al. [63] showed that for the same cell line and for various concentrations of Gd-based particles, the mean tail moment is greater than that obtained without particles. Hossain [126] and Zhang et al. [127], who studied the effect of bismuth nanoparticles on DNA damage in X-ray and Cs-137 irradiated HeLa cells, respectively, came to similar conclusions - i.e. that NPs enhance DNA damage as measured by comet tail moment. All of these groups assessed the NP-enhanced DNA damage based on the size and moment of the comet tail according to [128] and compared the results to samples irradiated without NP. Only Miladi et al. [125] investigated the effect of NPs with comet assay for more than one dose level. However, no attempt to quantify dose dependency related to NP presence was made.
Gel electrophoresis on plasmid DNA
A small number of groups have evaluated the radiobiological effect of gold NPs using plasmid DNA [129-132]. This assay allows one to quantify the effect of radiation on basic DNA systems in the presence or not of NPs and is a powerful tool for undertaking mechanistic studies of the process of DNA damage induced by NPs in combination with radiation. On the other hand, the plasmids are very simple systems and, therefore, such structures are quite different from the mammalian cells. DNA damage is generally determined by separating and quantifying different conformations of plasmid DNA through agarose gel electrophoresis. Gel electrophoresis on plasmid DNA is an established technique for quantification of single strand breaks (SSB) and double strand breaks (DSB) in simple biological systems and even though the method is based on a simple biological system, the technique is supported by a robust quantification methodology which has been used and validated with various radiation qualities [133, 134].
Following such protocols, Butterworth et al. [129], Brun et al. [130] and others quantified the strand break formation by calculating the chemical yield (G) based on a target mass consisting of the plasmid DNA, as previously described by Purkayastha et al. [135]. Specifically, the DNA break (SSB and DSB) yields measured through gel electrophoresis were plotted as a logarithm of the fraction of undamaged supercoiled-DNA (scDNA) as a function of radiation dose and fitting it to a straight line. The radiation yields (G), quantifying the number of breaks per joule of absorbed energy, for single- and double-strand breaks (G(SSB) and G(DSB)), were calculated from the slopes of straight lines. From these values, dose modifying factors (DMF) for given NP concentrations were calculated as a ratio of G values with and without NPs.
Alternative quantification approaches have also been reported. Zheng et al. [132] evaluated the reported results in terms of quantum yields, Y, defined as the number of DNA damages per incident 60 keV electron per DNA molecule. Quantum yields for the induction of SSB and DSB were derived from the initial slopes of the dose response curves with the yield of SSB and DSB measured again through gel electrophoresis. The enhancement due to NPs was quantified as ratio of the SSB and DSB induction probabilities for samples irradiated with and without NPs. Foley et al. [131], on the other hand, calculated the relative enhancement ratio as a ratio of the percentage of the relaxed DNA in the NP-bound scDNA to that of the relaxed DNA in free scDNA. However, the authors did not specify in their work how the quantities of relaxed DNA were measured.
γ-H2AX and 53BP1
Response to radiation exposure can be assessed by measuring the yield of induced DNA DSBs and their repair as a function of time by employing immunofluorescence staining of the phosphorylated histone γ ‐H2AX [136-138] and the DNA repair protein 53BP1 [139, 140]. Phosphorylation of the H2AX histone and recruitment of 53BP1 protein are some of the initial steps in the cell machinery to repair DSBs and the use of fluorescent antibodies allows for formation of detectable (through fluorescence microscopy) foci which have been demonstrated to be in 1:1 ratio with the number of DBSs [138]. This forms the basis of a sensitive quantitative method for detection of DNA DSBs in mammalian cells [141, 142]. The assay is also suitable for investigating the DNA repair through monitoring the number of DSBs at different times following irradiation.
Among the reviewed literature (Table 4), γ-H2AX and 53BP1 assays have both been employed to investigate DNA damage in nanoparticle studies to quantify the yield of DSBs immediately after radiation exposure or at later stages, e.g. 24 or 48 hours post-irradiation. Direct comparison of published results remains difficult due to heterogeneity of approaches such as cell lines, radiation quality, background correction and scoring methods with hard to control automated and manual bias. Some studies have focused on the number of radiation induced lesions by monitoring DSBs shortly after irradiation (mainly 30 minutes or 1 hour [46, 62, 63, 143]) whilst others have looked at the residual damage fixing cells after 24 hours post irradiation [16, 43, 56, 144]. Results are generally reported in terms of induced number of foci (per nucleus per Gy) and consequently the NP enhancement has been expressed as ratio of the number of foci (N of FC) with and without NPs [46, 56, 63], corrected for the relative controls [144]. Depending on the objective of the study, the control samples were exposed only to irradiation or to NPs alone. For instance, Chattopadhyay et al. [46] measured DSB enhancement directly following irradiation as a ratio of N of foci following X-ray treatment with Au-NPs and control cells treated just with Au-NPs (without X-rays exposure), whilst Ngwa et al. [144] measured residual γ-H2AX foci (24 hour post-irradiation) as a ratio of foci in cells incubated with Au-NPs over those without (with both samples being irradiated). When the aim of the study is to quantify the foci enhancement due to the presence of NPs, the increase N of foci in the NP treated samples should be compared to that obtained for untreated samples. The ratio of N of foci in irradiated treated samples over the N of foci of irradiated untreated samples assumes that the presence of NPs does not alter the background N of foci. This assumption may not always be valid.
The vast majority of DNA damage studies [16, 43, 62, 63, 143] with NPs are reported to selected dose levels, often a single level below 2 Gy and the N of foci detected is then reported as average N of foci per cell nucleus per Gy. This is justified by the established direct proportionality between the N of DSBs induced and the dose absorbed in the dose range of clinical interest (<2 Gy). Due to the relatively small amount of NPs involved in these studies, such assumption can be considered valid also for NP treated samples. Although the majority of studies reported focus on the assessment of the extra N of foci immediately after irradiation (i.e. extra damage caused by the presence of NP) or at later stages (i.e. enhanced unrepaired fraction of DNA damage), significant information could also be drawn from analysing the DNA repair kinetic (i.e. monitoring the reduction in N of foci as a function of time post irradiation).
The theoretical model, developed to analyse and quantify the mechanism underlying the dynamics of irradiation induced foci and its decay, is based on an analytical approach which takes into account the foci phosphorylation and de-phosphorylation processes. The function
(11)
reported in previous work [145], is the product of two terms representing the competitive process of foci induction and decay as a function of time (t) after an acute irradiation. In the first term of the equation, A represents a normalization factor and B drives the dynamics of the induction whilst in the second term, C represents the amount of simple damage repairable with a fast kinetic (D) whilst (1-C) represents the more complex type of damage repairable with a slower kinetic with a decay rate E. Although repair rates and fraction of complex damage are key parameters to determine the biological outcomes, none of the investigations reported in the literature made an attempt to characterize how the DSBs repair kinetics are influenced by NPs.
Monte Carlo in NP studies
High-Z NPs potential as dose enhancing agent was initially believed to lie in their higher photoelectric absorption coefficient compared to water or soft tissue. While experimental in vitro studies provide evidence of Au-NPs radio-sensitizing properties, there is an apparent disparity between the observed experimental findings and the level of radio-sensitization predicted by mass-energy absorption and NP concentration [146]. Macroscopic theoretical predictions based on the ratio of the mass-energy absorption coefficients of gold and soft tissue suggest that following exposure to a keV photon source, the addition of 1% of gold by mass to the tumour would approximately double the dose absorbed [11, 147-149]. However, experimental data indicate that much smaller amounts of gold nanoparticle are required to produce effects equivalent to doubling the absorbed dose, highlighting the inadequacy of macroscopic models.
Various methods are available for calculating the dose distribution at micrometre and nanometre level resulting from a given irradiation and NP combination. The majority of theoretical studies investigating radio-sensitizing effects of high-Z nanoparticles make use of Monte Carlo methods to evaluate the dose distributions and predict the enhancement effects. In these methods, individual photon and electron interactions with matter are simulated in a probabilistic manner, based on measured cross-sections for a variety of physical interactions. Modelling all of the interactions of the primary and secondary particles allows to predict accurately dose depositions down to the micrometre and nanometre level. This provides a more realistic description of the impact of the presence of nanoparticles on the dose absorption and offers a powerful tool for assessing the change in biological effectiveness being related to the complexity of DNA lesions.
A variety of dedicated Monte Carlo packages such as EGSnrc [150], Geant4 [151], PENELOPE, MCNP5, MCNPX and NORTEC have been employed to study high-Z nanoparticle radio-enhancement (Table 5). These MC simulations were carried out in simplified geometries and provided a pilot set of data in support of high-Z nanoparticle radiotherapy. Apart from the above mentioned discrepancies between theoretical and experimental data, there are also inconsistencies between Monte Carlo studies carried out by different groups. This is mainly due to the complexity of the MC simulations, the strong requirements on accurate input parameters which are often only estimated on the basis of experimental data or replaced by macroscopic approximations and the use of different library data and electron cut-off energy thresholds.
Nanoparticle studies employing γ-H2AX and 53BP1 assays. In the “quantification of enhancement column” FC stands for “N of foci” and the subscript indicates: “NP+Irr” = irradiated samples treated with NPs, “NP” = un-irradiated samples treated with NPs, “Irr” = irradiated samples without NPs and “Cont” = un-irradiated samples without NP.
| Dose | Quantification of enhancement | Method of scoring | Time of fixing after radiation | Dynamics evaluated | Ref. |
|---|---|---|---|---|---|
| 0 - 1.1 Gy | FCNP+Irr / FCCont | Information not provided | 24 h | No | [144] |
| 5 Gy | FCNP+Irr / FCCont | ImageJ free macro | 1 h | No | [63] |
| 2 Gy | Qualitative foci level comparison | Information not provided | 1 h | No | [143] |
| 1 Gy | Qualitative foci level comparison | Information not provided | 30 min | No | [62] |
| 0.5 Gy | FCNP+Irr / FCCont | Customised ImageJ macro | 30 min | No | [46] |
| 2 Gy | Qualitative foci level comparison | Information not provided | 1 h, 24 h | No | [43] |
| 2 Gy | FCNP+Irr / FCCont | Manually under microscope view | 1 h, 24 h | No | [56] |
| 1 Gy | Qualitative foci level comparison | Information not provided | 1 h, 24 h | No | [16] |
Several MC calculations have been used to calculate the dose enhancement from gold nanoparticles at the macroscopic level (mm to cm scales) in response to clinical X-ray beams (see Table 5). The dose enhancement effects were characterized by considering numerous physical interactions and quantities, such as photoelectric absorption, properties of secondary electrons ejected from nanoparticles, photoelectric energy conversion, and physical dose ratios between irradiation with and without NPs. These studies included both external (LINACs, kV X-ray sources) and internal (brachytherapy) γ-ray sources. However, not all of the authors used the full photon spectra in their calculations, often simplifying the problem to mono-energetic beams. In these cases the Monte Carlo dose enhancement was defined as the increase of physical dose absorbed by the tumour volume when treated with nanoparticles (without estimation of the biological response) and was determined for various simplified geometries approximating clinical conditions without accounting for the energy deposition at sub-micrometre scales. Macroscopic simulations of coupled photon-electron transport on length scales much larger than an individual cell were performed using MC codes such as EGSnrc [147, 152, 153], Geant4 [154], MCNP5 [74, 155] or MCNPX [156] that employ the condensed history electron transport approximation. This technique is adequate for calculating the dose distributions on a macroscopic scale where the discrete energy losses are orders of magnitude larger than the electron binding energies (>1 keV). For most radiotherapy treatments this is an acceptable approximation, due to the sparsely ionising nature of X-rays and the relative homogeneity of organic matter.
Monte Carlo studies on radiation therapy enhancement by high-Z nanoparticles. In the “Dose enhancement” column  stands for MC-calculated absorbed dose by the tumour treated with NPs while
stands for MC-calculated absorbed dose by the tumour treated with NPs while 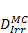 represents the absorbed dose in the tumour without NPs.
represents the absorbed dose in the tumour without NPs.
| MC code (electron cutoff energy) | Radiation & (Nanoparticle) | Simulation type | Medium | Dose enhancement | Reference |
|---|---|---|---|---|---|
| Geant4-DNA | 80 kVp 6 MV (Au-NP) | Step-by-step, all interactions simulated explicitly | Water, Au | 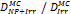 | [86] |
| MCNP5 (1 keV) PENELOPE 2008.1 (50 eV) | 300 kVp 6 MV 169Yb, 192Ir (Au-NP) | MCNP5: condensed histories method PENELOPE: step-by-step simulations | ICRU four-component soft tissue, Au | 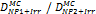 No control samples were simulated but energy deposition compared for different NPs | [74] |
| EGSnrc NORTEC (7.4 eV) | 125I 103Pd 169Yb, 192Ir 50 kVp 6 MV (Au-NP) | EGSnrc: condensed history method NORTEC: step-by-step simulations (electron step size <1 µm) | Water | 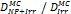 | [152] |
| PENELOPE | 200 kVp 1 MV 6 MV (Hafnium oxide-NP) | Step-by-step simulations | Water with (Hafnium oxide -NP) | 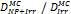 | [57] |
| Geant4-DNA | 20-150 kVp 160 kVp (Au-NP) | Step-by-step simulations | Water, Au | Relative Biological Effectiveness (RBE) calculated through Local Effect Model (LEM) | [44] |
| MCNPX v.2.6.0 (1 keV) | 50-120 keV Co-60 6 MV 18 MV (Au-NP) | Condensed histories method | Water, Au | 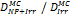 | [156] |
| Geant4 (250 eV) | 68 kVp 82 kVp 2 MV (Au-NP) | Condensed histories method | Water, Au | 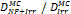 | [159] |
| Geant4 | 192Ir (Au-NP) | Condensed histories method | Water, Au | 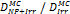 | [160] |
| Geant4 (250 eV) | 20 kVp 100 kVp (Au-NP) | Condensed histories method | Water, Au | 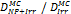 | [154] |
| MCNP5 (1 keV) | 125Ir 50 kVp 169Yb (Au-NP) | Condensed histories method | ICRU four-component soft tissue, Au | 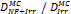 | [155] |
| Geant4 | 50, 250 keV, 1, 4 MeV Electrons (Au-NP) | Condensed histories method | Water, Au | 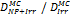 | [161] |
| EGSnrc (1 keV) Geant4 (250 eV) | 40 kVp 100 kVp 1000 kVp 6 MV (Au-NP) | Condensed histories method | Water, Au | 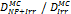 | [153] |
| EGSnrc (10 keV) MCNP5 (1 keV) | 140 kVp 4 MV 6 MV 125Ir (Au-NP) | Condensed histories method | ICRU four-component soft tissue, Au | 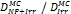 | [147] |
| Not stated | 100 kVp | Not stated | Water, Au | Enhancement factor reported, but no details provided | [162] |
However, it is well established that dose distributions on the microscopic scale can have significant impact on the biological response. For instance, heavy charged particles deliver a highly inhomogeneous distribution of energy on the sub-cellular scale, which leads to much higher probabilities of multiple damage, which, in consequence, may produce complex DSBs and thus enhance cell death [157]. Although such dense ionising events are rare in therapies which make use of MV X-rays, the combination of photons with NPs may significantly alter the microscopic and nanoscopic pattern of typical dose distribution obtained with X-ray irradiation. This hypothesis has motivated authors to perform simulations in NP studies using MC codes allowing to set up low energy cut-offs which enable explicit simulation of interactions on a nanoscale level. This type of transport is implemented in tools such as PENELOPE [74], NORTEC [152] and Geant4-DNA [44, 86], the latter being of the largest interest. The Geant4-DNA extension has been developed to calculate step-by-step radiation track structures for electrons, protons, alpha particles and heavy ions on a nanometre scale. Therefore, this tool plays a vital role in nano-dosimetry work necessary for simulating the production of DNA double strand breaks. The Geant4-DNA processes are all discrete, thus they simulate explicitly all interactions and use analytical and semi-empirical cross sections which cover the electron energy range from 0.026 eV (corresponding to electron thermalization) up to 10 keV. Although the quality of the model has been experimentally verified for energies down to 1 keV by Incerti et al. [158], there is little experimental data to confirm its validity below this energy. It should also be noted that the Geant4-DNA toolkit considers particle interactions in a water medium only, due to limited amounts of experimental data for verification and semi-empirical model development. Although water is the primary component of cells, the currently implemented model does not consider the highly scavenging cellular environment.
For doses typically used in radiotherapy, over 99% of the nanoparticles present in a system would not contribute to the dose-modifying effects [44] as they would not directly interact with the incoming radiation beam (although all NPs may interfere with cellular processes and therefore indirectly affect the radiation response). This highlights the limitations of averaging the dose-modifying effect over large volumes containing many NPs as it would result in a relatively homogeneous distribution of additional dose spread uniformly across the cell, despite little or no effect would be seen near most NPs and with dramatic dose spikes in the vicinity of the few which do interact with the radiation beam. Therefore, in order to calculate dose enhancement, which in this case refers to the difference in dose with/without NPs to produce a given level of biological effect, rather than the ratio of physical absorbed doses, it is necessary to carry out MC calculations in two stages. In the first (macroscopic) stage of the simulation the X-rays are transported across macroscopic depths (mm to cm) to a location near the target NP in a homogeneous medium where the phase space is determined. In the second (microscopic) stage, the previously generated phase space is used as the source for a new MC simulation to determine the microscopic relevant dosimetric quantities. These quantities together with the macroscopic dose absorption level will determine the cellular radiation response through the use of conventional radiobiological models such as the Local Effect Model (LEM) [44]. Such simulations will therefore provide theoretical output which can be cross checked against experimental data. Transition between the macroscopic and nanoscopic levels of simulation is essential in order to ensure that the magnitude of the computed dose enhancement effects is not misrepresented. This is because dose enhancement is very sensitive to beam quality [153] and thus it may depend on the specific simulation geometry as well as on the angular component of the microscopic phase space used in the second stage.
Finally, it must be noted that in MC simulations, there are two different types of systematic uncertainties affecting the outcome of the results. The first type of uncertainty is related to limitations of the physical model used to simulate a given physical process. The second type of uncertainty is related to the limitation of the MC method itself. The MC method generally is a numerical approach which is used to simulate the physical world. For an accurate simulation, the particle position and the momentum of each particle must be known with accuracy. Below 1 keV, quantum mechanics becomes more dominant, and the position and the momentum of the particles are not known accurately because of uncertainty principle. MC codes cannot take into account these effects due to the way the numerical method works, therefore these issues may lead to systematic uncertainties.
Discussion
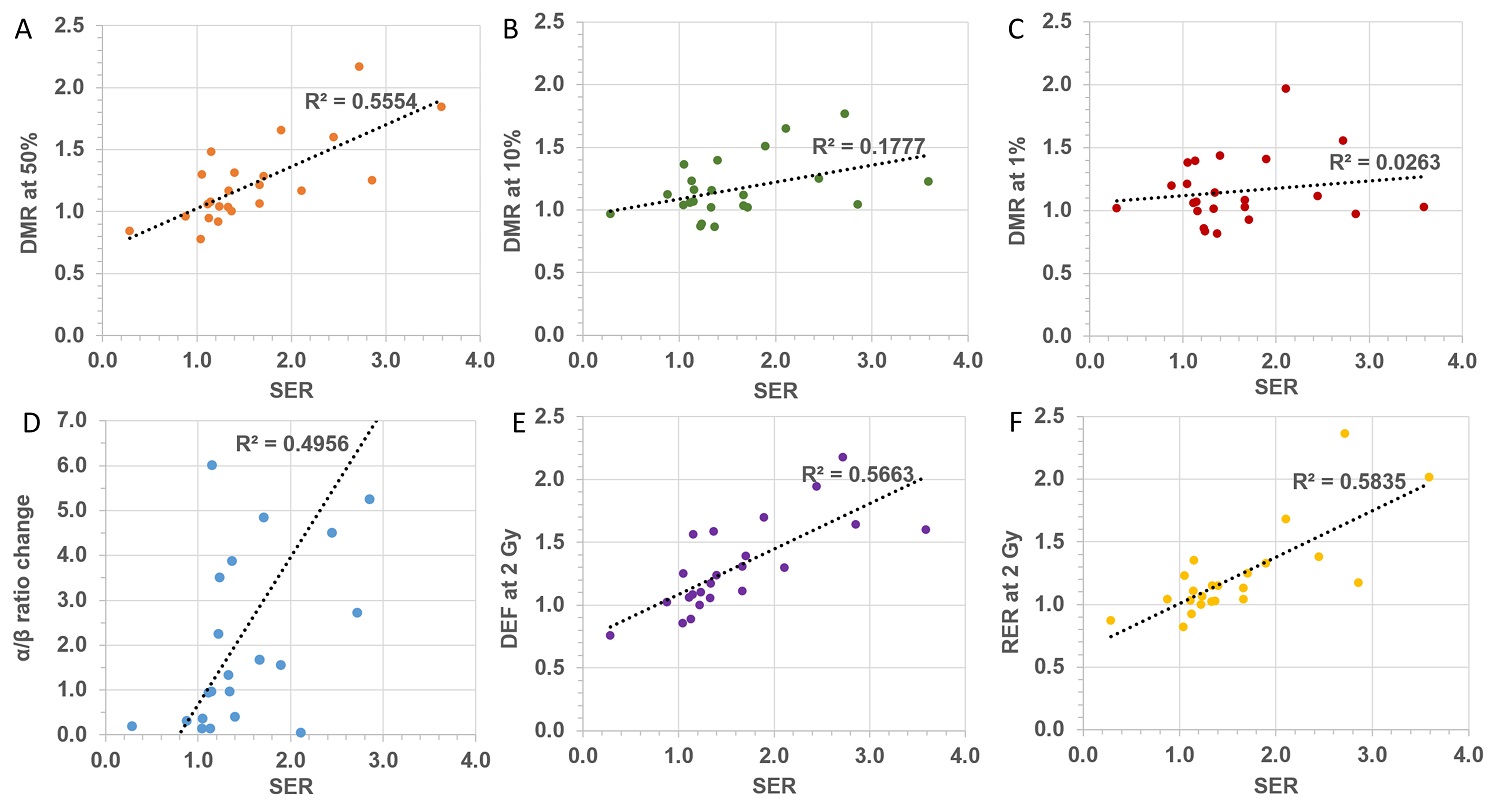
Cell survival is the “gold standard” assay for radiobiology and consequently it has been extensively employed for assessment of the impact of NPs on radiation effects. However, attempts to quantify the enhancement caused by NPs seem to have generated confusion and have led to a multitude of parameters being defined, often with conflicting terminology. Although some of these parameters may be particularly meaningful in elucidating specific underlying mechanistic actions, it is worth stressing that the ICRU recommends considering the whole survival curve rather than single point measurements for the evaluation of changes in biological effectiveness. In this respect, the sensitizer enhancement ratio (SER), defined through the mean dose inactivation (MID), appears to be a suitable approach to provide a single parameter to quantify the impact of NPs on the in vitro survival curves. It must be remembered that any quantification is specific for a given experimental setup which includes NP type, concentration, cell line and radiation quality. From the available NP studies, we collected α and β parameters to explore the relation between the various NP-enhancement factors reported in the literature. Interestingly, there does not appear to be any strong correlation between the different quantification methods currently employed, as evidenced by the poor correlation coefficient shown in Figure 2. Such a lack of correlation reflects the fact that each parameter is related to a particular feature of the survival curve and cannot be used as surrogate for any of the other parameters. This further highlights the need for a standardized approach to quantify the radiobiological effect of NPs. Due to the physical and chemical changes at the nanoscale level caused by NPs when exposed to ionizing radiation, it is essential to determine the amount of nanoparticles being absorbed by the cells, as well as their sub-cellular distribution. This is in line with current theranostic strategies targeting specific sub-cellular compartments [163]. When possible, radiobiological investigations should be accompanied by quantification of the amount of NPs present in the cells at the time of the radiation exposure. Finally, it is critical to point out that cellular radiation response is the result of complex molecular processes and any agent impinging on such pathways will consequently affect the radiation response. It is therefore necessary to supplement the radiobiological investigations with analysis of the impact of NPs on cellular activities (such as cell cycle) in order to understand the mechanisms regulating radio-sensitization.
With regard to the production of reactive oxygen species, a significant number of studies have used fluorescence assays to provide a relative assessment of the variation of ROS caused by the presence of NPs in the irradiated cells. Using a variety of approaches, authors have usually reported the relative fluorescence values as a ratio of fluorescence of NP treated cells over fluorescence of un-treated cells with both samples being irradiated. Although this parameter may provide indication of the effect caused by NPs, comparison with the fluorescence levels of un-irradiated samples (treated and un-treated with NPs) should also be reported to assess the impact of NPs on the cellular system. This is critical to evaluate possible synergies or simply additive effects between NPs and radiation. Aside from the differences in the technical modalities in which the fluorescence signal has been acquired and measured, there is also a general lack of investigation into the effect as a function of dose. This is based on the assumption of a linear production of ROS as a function of dose which is yet to be validated in presence of NPs. Compared to established radiation chemistry mechanisms, recent investigations [164] seem to suggest additional pathways for the formation of ROS in the presence of NPs which could lead to non-linearity in the yield of ROS as a function of dose. Reports of the relative fluorescence at different dose levels would therefore be advocated. In general, no rigorous ROS quantification in absolute terms is possible using fluorescence assays in cells [107] and relative assessments suffer from lack of recommendation on the fluorescence measurements, as well as guidance for the comparison with control samples.
The coumarin assay would appear to be a more robust methodology for quantifying the hydroxyl radical in bulk solutions. Although precautions need to be taken in either removing the NPs before the coumarin intensity measurements or accurately estimating its quenching effect. Adaptation of the established coumarin assay to use with NPs represents a potentially powerful method for investigating the radiation chemistry mechanisms which underpin the radiobiological response with NPs. The assay also offers the possibility of absolute quantification of the yield of OH radicals being produced, though this requires detailed knowledge of the impact of NPs on the coumarin-OH affinity, which is likely to depend on the NP type.
Correlation between different quantification factors: (A) DMR at 50% survival, (B) DMR at 10% survival, (C), DMR at 1% survival, (D) α/β ratio, (E) DEF at 2 Gy, (F) RER at 2 Gy as a function SER.
Assessment of DNA damage is a key aspect of any mechanistic radiobiological investigation and several established assays have been used for NP studies. Although qualitative indications can be drawn from the comet assay, no attempts have so far been made to quantify the nanoparticle mediated enhancement factor in terms of total amount of DNA damage in any of the reported studies. This is primarily due to the difficulties in extracting robust quantitative information regarding the number of DNA breaks from the comet assay [131] and the lack of validation of the technique for use with NPs (i.e. impact of NPs on DNA migration fluorescence readout in electrophoresis). Gel electrophoresis on plasmid DNA, on the other hand, is an established technique for quantification of SSBs and DSBs in simple biological systems. Even though the method is based on a simple biological system, the technique is supported by a robust quantification methodology which has been used and validated with various radiation qualities. Extrapolation to cellular environment may not be straightforward but this technique could be valuable for elucidating mechanistic processes. Finally, immunofluorescence assays can provide key information on both the rate of DNA breaks and repair. The main limitations of such assays lay in the scoring process, which strongly depends on the imaging setup (i.e. issue with 3D scoring and foci overlap) and the operator skills and expertise with automated systems still not fully validated and manual foci scoring is subject to bias and objective interpretation. Adaptation of such assays to NP studies appear to be straightforward and quantification of the NP effect could be extracted based on the number of foci detected (i.e. DNA DSBs) both in terms of damage induced and residual. The assay could also provide insights on the impact of NPs on the efficiency of the DNA repair pathways by using established repair kinetic models.
Finally, the use of Monte Carlo simulations is a unique powerful tool to investigate the changes in spatial distribution of dose deposition induced by NPs down to the nanometre scale (i.e. DNA level). This is a fundamental aspect in understanding if and how NPs alter the biological effectiveness of the incident radiation. Such simulations can generate useful micro-dosimetric parameters which should then be cross-checked against experimental data through established radiobiological models. Although Monte Carlo codes have been extensively benchmarked and validated for conventional dosimetry purposes, application to very low energy thresholds and nanometre scale levels are still subjected to potentially large uncertainties. Furthermore, detailed representation of the radiation source and samples (i.e. NP geometry, composition, environment etc.) is essential for accurate estimation of the physical processes. Such information may not always be available.
In conclusion, a wide range of experimental and theoretical tools are available to assess the radiobiological impact of NPs and have been employed to generate a substantial amount of data. However, data reported in the literature highlight the difficulty in identifying suitable parameters for quantification of the NP mediated effect and confusion owing to lack of recommendations and standardization of approaches. The present review aims to summarise methods employed so far, pointing out their strengths and limitations for the establishment of a dedicated methodology suitable to quantitatively investigate the unique radiobiological properties of high-Z nanoparticles, i.e. radiosensitizers and radiation modifiers.
Abbreviations
NP: nanoparticle; Au: gold; ICRU: International Commission on Radiation Units and Measurements; MID: mean inactivation dose; SF: survival fraction; D: dose; MTT : methyl-thiazol-tetrazolium; LQ: linear-quadratic; SER: sensitizer enhancement ratio; Cont: control; DMR: dose modifying ratio; DMF: dose modifying factor; DEF: dose enhancement factor; REF: radio-sensitivity enhancement factor; RER: radiation enhancement ratio; ROS: reactive oxygen species; LET: linear energy transfer; FIR: fluorescence intensity ratio; SSB: single-strand breaks; DSB: double-strand breaks; N: number; MC: Monte Carlo; Au-NP: gold nanoparticle; LEM: Local Effect Model.
Acknowledgements
This work was supported by the Innovation Research and Development programme of the National Physical Laboratory, grant N 118084. We would like to acknowledge Graham Bass and Thorsten Sander for reviewing the manuscript and their valuable suggestions that we added to this text.
Competing Interests
The authors have declared that no competing interest exists.
References
1. CTRad: National Leadership in Radiotherapy Research, Achievements and Vision. London, UK: National Cancer Research Institute. http://www.ncri.org.uk/wp-content/uploads/2014/10/2014-CTRad-Achievements-and-vision-WEB.pdf
2. Ferlay J, Soerjomataram I, Dikshit R. et al. Cancer incidence and mortality worldwide: Sources, methods and major patterns in GLOBOCAN 2012. International Journal of Cancer. 2015;136:E359-E86
3. NHS Imaging and Radiodiagnostic activity in England. Leeds, UK: NHS England. https://www.england.nhs.uk/statistics/wp-content/uploads/sites/2/2013/04/KH12-release-2012-13.pdf
4. Berrington de González A, Mahesh M, Kim K. Projected cancer risks from computed tomographic scans performed in the United States in 2007. Archives of Internal Medicine. 2009;169:2071-7
5. WHO Global Initiative on Radiation Safety in Health Care Settings. Geneva, Switzerland: WHO. http://www.who.int/ionizing_radiation/about/med_exposure/en/
6. Mello RS, Callisen H, Winter J. et al. Radiation dose enhancement in tumors with iodine. Medical Physics. 1983;10:75-8
7. Norman A, Adams FH, Riley RF. Cytogenetic Effects of Contrast Media and Triiodobenzoic Acid Derivatives in Human Lymphocytes. Radiology. 1978;129:199-203
8. Adams FH, Norman A, Mello RS. et al. Effect of Radiation and Contrast Media on Chromosomes. Radiology. 1977;124:823-6
9. Matsudaira H, Ueno AM, Furuno I. Iodine contrast medium sensitizes cultured mammalian cells to X rays but not to gamma rays. Radiation Research. 1980;84:144-8
10. Mesa AV, Norman A, Solberg TD. et al. Dose distributions using kilovoltage x-rays and dose enhancement from iodine contrast agents. Physics in Medicine and Biology. 1999;44:1955-68
11. Robar JL, Riccio SA, Martin MA. Tumour dose enhancement using modified megavoltage photon beams and contrast media. Physics in Medicine and Biology. 2002;47:2433-49
12. Peer D, Karp JM, Hong S. et al. Nanocarriers as an emerging platform for cancer therapy. Nature Nanotechnology. 2007;2:751-60
13. Chen J, Saeki F, Wiley BJ. et al. Gold nanocages: Bioconjugation and their potential use as optical imaging contrast agents. Nano Letters. 2005;5:473-7
14. Yang PH, Sun XS, Chiu JF. et al. Transferrin-mediated gold nanoparticle cellular uptake. Bioconjugate Chemistry. 2005;16:494-6
15. Hainfeld JF, Slatkin DN, Smilowitz HM. The use of gold nanoparticles to enhance radiotherapy in mice. Physics in Medicine and Biology. 2004;49:N309-15
16. Jain S, Coulter JA, Hounsell AR. et al. Cell-specific radiosensitization by gold nanoparticles at megavoltage radiation energies. International Journal of Radiation Oncology Biology Physics. 2011;79:531-9
17. Chithrani DB, Jelveh S, Jalali F. et al. Gold nanoparticles as radiation sensitizers in cancer therapy. Radiation Research. 2010;173:719-28
18. Chattopadhyay N, Cai Z, Pignol J-P. et al. Design and Characterization of HER-2-Targeted Gold Nanoparticles for Enhanced X-radiation Treatment of Locally Advanced Breast Cancer. Molecular Pharmaceutics. 2010;7:2194-206
19. Kassis AI. Therapeutic radionuclides: Biophysical and radiobiologic principles. Seminars in Nuclear Medicine. 2008;38:358-66
20. Schuemann J, Berbeco R, Chithrani DB. et al. Roadmap to Clinical Use of Gold Nanoparticles for Radiation Sensitization. International Journal of Radiation Oncology Biology Physics. 2016;94:189-205
21. Her S, Jaffray DA, Allen C. Gold nanoparticles for applications in cancer radiotherapy: Mechanisms and recent advancements. Advanced Drug Delivery Reviews. 2015 in press
22. Kumar R, Korideck H, Ngwa W. et al. Third generation gold nanoplatform optimized for radiation therapy. Translational Cancer Research. 2013;2:1-18
23. Butterworth KT, McMahon SJ, Taggart LE. et al. Radiosensitization by gold nanoparticles: effective at megavoltage energies and potential role of oxidative stress. Translational Cancer Research. 2013;2:269-79
24. Kwatra D, Venugopal A, Anant S. Nanoparticles in radiation therapy: a summary of various approaches to enhance radiosensitization in cancer. Translational Cancer Research. 2013;2:330-42
25. Retif P, Pinel S, Toussaint M. et al. Nanoparticles for Radiation Therapy Enhancement: the Key Parameters. Theranostics. 2015;5:1030-44
26. Puck TT, Marcus PI. Action of X-Rays on Mammalian Cells. The Journal of Experimental Medicine. 1956;103:653-66
27. Rafehi H, Orlowski C, Georgiadis GT. et al. Clonogenic Assay: Adherent Cells. Jove-Journal of Visualized Experiments. 2011;13:1-3
28. Franken NAP, Rodermond HM, Stap J. et al. Clonogenic assay of cells in vitro. Nature Protocols. 2006;1:2315-9
29. Buch K, Peters T, Nawroth T. et al. Determination of cell survival after irradiation via clonogenic assay versus multiple MTT Assay - A comparative study. Radiation Oncology. 2012;7:1-6
30. Safora N, Bijan H. MTT assay instead of the clonogenic assay in measuring the response of cells to ionizing radiation. Journal of Radiobiology. 2014;1:3-8
31. Hall EJ, Giaccia AJ. Radiobiology for the Radiologist. Philadelphia: Lippincott Williams & Wilkins. 2012
32. ICRU. Quantitative Concepts and Dosimetry in Radiobiology ( Report no. 30). Measurement International Commission on Radiation Units and. Washington, DC. 1979
33. Kellerer AM, Hug O. Theory of dose-effect relations. Heidelberg: Springer. 1972
34. Kellerer AM. Statistical and Biophysical Aspects of the Survival Curve. Proceedings of the Sixth L Η Gray Conference. 1975 Chapter 2: 69-77
35. Fertil B, Dertinger H, Courdi A. et al. Mean inactivation dose: a useful concept for intercomparison of human cell survival curves. Radiation Research. 1984;99:73-84
36. Jain S, Coulter JA, Butterworth KT. et al. Gold nanoparticle cellular uptake, toxicity and radiosensitisation in hypoxic conditions. Radiotherapy and Oncology. 2014;110:342-7
37. McMahon SJ, Hyland WB, Muir MF. et al. Nanodosimetric effects of gold nanoparticles in megavoltage radiation therapy. Radiotherapy and Oncology. 2011;100:412-6
38. Wang C, Li X, Wang Y. et al. Enhancement of radiation effect and increase of apoptosis in lung cancer cells by thio-glucose-bound gold nanoparticles at megavoltage radiation energies. Journal of Nanoparticle Research. 2013:15
39. Liu SK, Coackley C, Krause M. et al. A novel poly(ADP-ribose) polymerase inhibitor, ABT-888, radiosensitizes malignant human cell lines under hypoxia. Radiotherapy and Oncology. 2008;88:258-68
40. Wang C, Jiang Y, Li X. et al. Thioglucose-bound gold nanoparticles increase the radiosensitivity of a triple-negative breast cancer cell line (MDA-MB-231). Breast Cancer. 2015;22:413-20
41. Cui L, Tse K, Zahedi P. et al. Hypoxia and cellular localization influence the radiosensitizing effect of gold nanoparticles (AuNPs) in breast cancer cells. Radiation Research. 2014;182:475-88
42. Rahman WN, Corde S, Yagi N. et al. Optimal energy for cell radiosensitivity enhancement by gold nanoparticles using synchrotron-based monoenergetic photon beams. International Journal of Nanomedicine. 2014;9:2459-67
43. Mirjolet C, Papa AL, Crehange G. et al. The radiosensitization effect of titanate nanotubes as a new tool in radiation therapy for glioblastoma: A proof-of-concept. Radiotherapy and Oncology. 2013;108:136-42
44. McMahon SJ, Hyland WB, Muir MF. et al. Biological consequences of nanoscale energy deposition near irradiated heavy atom nanoparticles. Scientific Reports. 2011;1:1-9
45. Bobyk L, Edouard M, Deman P. et al. Photoactivation of gold nanoparticles for glioma treatment. Nanomedicine-Nanotechnology Biology and Medicine. 2013;9:1089-97
46. Chattopadhyay N, Cai Z, Kwon YL. et al. Molecularly targeted gold nanoparticles enhance the radiation response of breast cancer cells and tumor xenografts to X-radiation. Breast Cancer Research and Treatment. 2013;137:81-91
47. Jeynes JC, Merchant MJ, Spindler A. et al. Investigation of gold nanoparticle radiosensitization mechanisms using a free radical scavenger and protons of different energies. Physics in Medicine and Biology. 2014;59:6431-43
48. Zhang X-D, Wu D, Shen X. et al. Size-dependent radiosensitization of PEG-coated gold nanoparticles for cancer radiation therapy. Biomaterials. 2012;33:6408-19
49. Rahman WN, Bishara N, Ackerly T. et al. Enhancement of radiation effects by gold nanoparticles for superficial radiation therapy. Nanomedicine. 2009;5:136-42
50. Kaur H, Pujari G, Semwal MK. et al. In vitro studies on radiosensitization effect of glucose capped gold nanoparticles in photon and ion irradiation of HeLa cells. Nuclear Instruments & Methods in Physics Research Section B-Beam Interactions with Materials and Atoms. 2013;301:7-11
51. Deacon J, Peckham M, Steel G. The radioresponsiveness of human tumours and the initial slope of the cell survival curve. Radiotherapy and Oncology. 1984;2:317-23
52. Fertil B, Malaise EP. Inherent cellular radiosensitivity as a basic concept for human tumor radiotherapy. International Journal of Radiation Oncology Biology Physics. 1981;7:621-9
53. Bristow RG, Hill RP. Comparison between in vitro radiosensitivity and in vivo radioresponse in murine tumor cell lines. II. In vivo radioresponse following fractionated treatment and in vitro/in vivo correlations. International Journal of Radiation Oncology Biology Physics. 1990;18:331-45
54. Coulter JA, Jain S, Butterworth KT. et al. Cell type-dependent uptake, localization, and cytotoxicity of 1.9 nm gold nanoparticles. International Journal of Nanomedicine. 2012;7:2673-85
55. Chien CC, Wang CH, Hua TE. et al. Synchrotron x-ray synthesized gold nanoparticles for tumor therapy. In: (ed.) Choi J. Y. Synchrotron Radiation Instrumentation, Pts 1 and 2; 2007. p. 1908-11
56. Taggart LE, McMahon SJ, Currell FJ. et al. The role of mitochondrial function in gold nanoparticle mediated radiosensitisation. Cancer Nanotechnology. 2014;5:5
57. Maggiorella L, Barouch G, Devaux C. et al. Nanoscale radiotherapy with hafnium oxide nanoparticles. Future Oncology. 2012;8:1167-81
58. Cui F-B, Li R-T, Liu Q. et al. Enhancement of radiotherapy efficacy by docetaxel-loaded gelatinase-stimuli PEG-Pep-PCL nanoparticles in gastric cancer. Cancer Letters. 2014;346:53-62
59. Khoshgard K, Hashemi B, Arbabi A. et al. Radiosensitization effect of folate-conjugated gold nanoparticles on HeLa cancer cells under orthovoltage superficial radiotherapy techniques. Physics in Medicine and Biology. 2014;59:2249-63
60. Joh DY, Sun L, Stangl M. et al. Selective Targeting of Brain Tumors with Gold Nanoparticle-Induced Radiosensitization. Plos One. 2013;8:1-10
61. Detappe A, Kunjachan S, Rottmann J. et al. AGuIX nanoparticles as a promising platform for image-guided radiation therapy. Cancer Nanotechnology. 2015;6:1-9
62. Butterworth KT, Coulter JA, Jain S. et al. Evaluation of cytotoxicity and radiation enhancement using 1.9 nm gold particles: potential application for cancer therapy. Nanotechnology. 2010;21:295101
63. Mowat P, Mignot A, Rima W. et al. In Vitro Radiosensitizing Effects of Ultrasmall Gadolinium Based Particles on Tumour Cells. Journal of Nanoscience and Nanotechnology. 2011;11:7833-9
64. Chen N, Yang W, Bao Y. et al. BSA capped Au nanoparticle as an efficient sensitizer for glioblastoma tumor radiation therapy. Royal Society of Chemistry Advances. 2015;5:40514-20
65. Wolfe T, Chatterjee D, Lee J. et al. Targeted gold nanoparticles enhance sensitization of prostate tumors to megavoltage radiation therapy in vivo. Nanomedicine: Nanotechnology, Biology and Medicine. 2015;11:1277-83
66. Kang B, Mackey MA, El-Sayed MA. Nuclear Targeting of Gold Nanoparticles in Cancer Cells Induces DNA Damage, Causing Cytokinesis Arrest and Apoptosis. Journal of the American Chemical Society. 2010;132:1517-9
67. Mahmoudi M, Azadmanesh K, Shokrgozar MA. et al. Effect of Nanoparticles on the Cell Life Cycle. Chemical Reviews. 2011;111:3407-32
68. Kim JA, Aberg C, de Carcer G. et al. Low Dose of Amino-Modified Nanoparticles Induces Cell Cycle Arrest. American Chemical Society Nano. 2013;7:7483-94
69. Mackey MA, Saira F, Mahmoud MA. et al. Inducing Cancer Cell Death by Targeting Its Nucleus: Solid Gold Nanospheres versus Hollow Gold Nanocages. Bioconjugate Chemistry. 2013;24:897-906
70. Butterworth KT, McMahon SJ, Currell FJ. et al. Physical basis and biological mechanisms of gold nanoparticle radiosensitization. Nanoscale. 2012;4:4830-8
71. Roa W, Zhang X, Guo L. et al. Gold nanoparticle sensitize radiotherapy of prostate cancer cells by regulation of the cell cycle. Nanotechnology. 2009:20
72. Wilson GD. Probing the Cell Cycle with Flow Cytometry. Journal of Biomedical Science and Engineering. 2014;7:698-711
73. Liu Y, Liu X, Jin X. et al. The dependence of radiation enhancement effect on the concentration of gold nanoparticles exposed to low- and high-LET radiations. Physica Medica-European Journal of Medical Physics. 2015;31:210-8
74. Lechtman E, Chattopadhyay N, Cai Z. et al. Implications on clinical scenario of gold nanoparticle radiosensitization in regards to photon energy, nanoparticle size, concentration and location. Physics in Medicine and Biology. 2011;56:4631-47
75. Fischer HC, Liu L, Pang KS. et al. Pharmacokinetics of nanoscale quantum dots: In vivo distribution, sequestration, and clearance in the rat. Advanced Functional Materials. 2006;16:1299-305
76. Scheffer A, Engelhard C, Sperling M. et al. ICP-MS as a new tool for the determination of gold nanoparticles in bioanalytical applications. Analytical and Bioanalytical Chemistry. 2007;390:249-52
77. Chithrani BD, Ghazani AA, Chan WCW. Determining the size and shape dependence of gold nanoparticle uptake into mammalian cells. Nano Letters. 2006;6:662-8
78. ICP-OES vs ICP-MS: A Comparison. Evans Analytical Group. http://www.eag.com/mc/icp-oes-vs-icp-ms.html
79. Liu C-J, Wang C-H, Chien C-C. et al. Enhanced x-ray irradiation-induced cancer cell damage by gold nanoparticles treated by a new synthesis method of polyethylene glycol modification. Nanotechnology. 2008:19
80. Zhang X, Xing JZ, Chen J. et al. Enhanced radiation sensitivity in prostate cancer by gold-nanoparticles. Clinical and Investigative Medicine. 2008;31:E160-7
81. Geng F, Song K, Xing JZ. et al. Thio-glucose bound gold nanoparticles enhance radio-cytotoxic targeting of ovarian cancer. Nanotechnology. 2011:22
82. Khan JA, Pillai B, Das TK. et al. Molecular effects of uptake of gold nanoparticles in HeLa cells. ChemBioChem. 2007;8:1237-40
83. Kong T, Zeng J, Wang X. et al. Enhancement of radiation cytotoxicity in breast-cancer cells by localized attachment of gold nanoparticles. Small. 2008;4:1537-43
84. Sim L, Fielding A, English M. et al. Enhancement of biological effectiveness of radiotherapy treatments of prostate cancer cells in vitro using gold nanoparticles. 2011 International Nanomedicine Conference. Coogee Beach, Sydney, N.S.W. 2011
85. Hossain M, Su M. Nanoparticle Location and Material-Dependent Dose Enhancement in X-ray Radiation Therapy. Journal of Physical Chemistry C. 2012;116:23047-52
86. Douglass M, Bezak E, Penfold S. Monte Carlo investigation of the increased radiation deposition due to gold nanoparticles using kilovoltage and megavoltage photons in a 3D randomized cell model. Medical Physics. 2013;40:1-9
87. Ward JF. DNA damage produced by ionizing radiation in mammalian cells: identities, mechanisms of formation, and reparability. Progress in Nucleic Acid Research and Molecular Biology. 1988;35:95-125
88. Townley HE, Rapa E, Wakefield G. et al. Nanoparticle augmented radiation treatment decreases cancer cell proliferation. Nanomedicine-Nanotechnology Biology and Medicine. 2012;8:526-36
89. Ito A, Nakano H, Kusano Y. et al. Contribution of indirect action to radiation-induced mammalian cell inactivation: Dependence on photon energy and heavy-ion LET. Radiation Research. 2006;165:703-12
90. Griffitt RJ, Weil R, Hyndman KA. et al. Exposure to copper nanoparticles causes gill injury and acute lethality in zebrafish (Danio rerio). Environmental Science & Technology. 2007;41:8178-86
91. Griffitt RJ, Luo J, Gao J. et al. Effects of particle composition and species on toxicity of metallic nanomaterials in aquatic organisms. Environmental Toxicology and Chemistry. 2008;27:1972-8
92. Karlsson HL, Cronholm P, Gustafsson J. et al. Copper oxide nanoparticles are highly toxic: A comparison between metal oxide nanoparticles and carbon nanotubes. Chemical Research in Toxicology. 2008;21:1726-32
93. Aruoja V, Dubourguier H-C, Kasemets K. et al. Toxicity of nanoparticles of CuO, ZnO and TiO2 to microalgae Pseudokirchneriella subcapitata. Science of the Total Environment. 2009;407:1461-8
94. Pujalte I, Passagne I, Brouillaud B. et al. Cytotoxicity and oxidative stress induced by different metallic nanoparticles on human kidney cells. Particle and Fibre Toxicology. 2011;8:2-16
95. van Den Berg AJJ, Halkes SBA, van Ufford HC. et al. A novel formulation of metal ions and citric acid reduces reactive oxygen species in vitro. Journal of Wound Care. 2003;12:413-8
96. Kadoma Y, Fujisawa S. Radical-Scavenging Activity of Thiols, Thiobarbituric Acid Derivatives and Phenolic Antioxidants Determined Using the Induction Period Method for Radical Polymerization of Methyl Methacrylate. Polymers. 2012;4:1025-36
97. Woolley JF, Stanicka J, Cotter TG. Recent advances in reactive oxygen species measurement in biological systems. Trends in Biochemical Sciences. 2013;38:556-65
98. Rothe G, Valet G. Flow cytometric analysis of respiratory burst activity in phagocytes with hydroethidine and 2',7'-dichlorofluorescin. Journal of Leukocyte Biology. 1990;47:440-8
99. Tarpey MM, Wink DA, Grisham MB. Methods for detection of reactive metabolites of oxygen and nitrogen: in vitro and in vivo considerations. American Journal of Physiology - Regulatory, Integrative and Comparative Physiology. 2004;286:R431-R44
100. Kalyanaraman B, Darley-Usmar V, Davies KJA. et al. Measuring reactive oxygen and nitrogen species with fluorescent probes: challenges and limitations. Free Radical Biology and Medicine. 2012;52:1-6
101. Johnston HJ, Hutchison GR, Christensen FM. et al. A critical review of the biological mechanisms underlying the in vivo and in vitro toxicity of carbon nanotubes: The contribution of physico-chemical characteristics. Nanotoxicology. 2010;4:207-46
102. Klein S, Sommer A, Distel LVR. et al. Superparamagnetic iron oxide nanoparticles as radiosensitizer via enhanced reactive oxygen species formation. Biochemical and Biophysical Research Communications. 2012;425:393-7
103. Klein S, Dell'Arciprete ML, Wegmann M. et al. Oxidized silicon nanoparticles for radiosensitization of cancer and tissue cells. Biochemical and Biophysical Research Communications. 2013;434:217-22
104. vanAcker S, vandenBerg DJ, Tromp M. et al. Structural aspects of antioxidant activity of flavonoids. Free Radical Biology and Medicine. 1996;20:331-42
105. Diaspro A, Chirico G, Usai C. et al. Photobleaching. Handbook of biological confocal microscopy. Springer. 2006:690-702
106. Tsien R, Waggoner A. Fluorophores for Confocal Microscopy. Photophysics and Photochemistry. Handbook of Biological Confocal Microscopy 2. Plenum Press, New York. 1995
107. Waters JC. Accuracy and precision in quantitative fluorescence microscopy. Journal of Cell Biology. 2009;185:1135-48
108. Wolf DE, Samarasekera C, Swedlow JR. Quantitative analysis of digital microscope images. Sluder G, editors. Digital Microscopy, 3rd Edition. 2007:365-96
109. Introduction to Flow Cytometry. A Learning Guide. 11-11032-01 Manual Part Number. San Jose, California. 2000
110. Geddes CD. Reviews in Fluorescence 2009. Springer Publishing Company, Incorporated. 2011
111. Sabatini CA, Pereira RV, Gehlen MH. Fluorescence modulation of acridine and coumarin dyes by silver nanoparticles. Journal of Fluorescence. 2007;17:377-82
112. Gomes A, Fernandes E, Lima J. Fluorescence probes used for detection of reactive oxygen species. Journal of Biochemical and Biophysical Methods. 2005;65:45-80
113. Uusitalo LM, Hempel N. Recent Advances in Intracellular and In Vivo ROS Sensing: Focus on Nanoparticle and Nanotube Applications. International Journal of Molecular Sciences. 2012;13:10660-79
114. Misawa M, Takahashi J. Generation of reactive oxygen species induced by gold nanoparticles under x-ray and UV Irradiations. Nanomedicine. 2011;7:604-14
115. David Gara P, Garabano N, Llansola Portoles M. et al. ROS enhancement by silicon nanoparticles in X-ray irradiated aqueous suspensions and in glioma C6 cells. Journal of Nanoparticle Research. 2012;14:1-13
116. Collins AK, Makrigiorgos GM, Svensson GK. Coumarin chemical dosimeter for radiation therapy. Medical Physics. 1994;21:1741-7
117. Manevich Y, Held KD, Biaglow JE. Coumarin-3-carboxylic acid as a detector for hydroxyl radicals generated chemically and by gamma radiation. Radiation Research. 1997;148:580-91
118. Yamashita S, Baldacchino G, Maeyama T. et al. Mechanism of radiation-induced reactions in aqueous solution of coumarin-3-carboxylic acid: Effects of concentration, gas and additive on fluorescent product yield. Free Radical Research. 2012;46:861-71
119. Sicard-Roselli C, Brun E, Gilles M. et al. A new mechanism for hydroxyl radical production in irradiated nanoparticle solutions. Small. 2014;10:3338-46
120. Gilles M, Brun E, Sicard-Roselli C. Gold nanoparticles functionalization notably decreases radiosensitization through hydroxyl radical production under ionizing radiation. Colloids and Surfaces B-Biointerfaces. 2014;123:770-7
121. Cheng NN, Starkewolf Z, Davidson RA. et al. Chemical Enhancement by Nanomaterials under X-ray Irradiation. Journal of the American Chemical Society. 2012;134:1950-3
122. Olive PL, Banath JP, Durand RE. Heterogeneity in radiation-induced DNA damage and repair in tumor and normal cells measured using the `comet' assay. Radiation Research. 1990;122:86-94
123. Olive PL. Cell proliferation as a requirement for development of the contact effect in Chinese hamster V79 spheroids. Radiation Research. 1989;117:79-92
124. Didenko VV. In Situ Detection of DNA Damage. Springer Protocols. 2002
125. Miladi I, Alric C, Dufort S. et al. The in vivo radiosensitizing effect of gold nanoparticles based MRI contrast agents. Small. 2014;10:1116-24
126. Hossain M. X-ray enabled detection and eradication of circulating tumor cells with nanoparticles. Orlando, Florida: University of Central Florida. 2012
127. Zhang X-D, Chen J, Luo Z. et al. Enhanced Tumor Accumulation of Sub-2 nm Gold Nanoclusters for Cancer Radiation Therapy. Advanced Healthcare Materials. 2014;3:133-41
128. Olive PL, Banath JP. The comet assay: a method to measure DNA damage in individual cells. Nature Protocols. 2006;1:23-9
129. Butterworth KT, Wyer JA, Brennan-Fournet M. et al. Variation of strand break yield for plasmid DNA irradiated with high-Z metal nanoparticles. Radiation Research. 2008;170:381-7
130. Brun E, Sanche L, Sicard-Roselli C. Parameters governing gold nanoparticle X-ray radiosensitization of DNA in solution. Colloids and Surfaces B-Biointerfaces. 2009;72:128-34
131. Foley EA, Carter JD, Shan F. et al. Enhanced relaxation of nanoparticle-bound supercoiled DNA in X-ray radiation. Chemical Communications. 2005:3192-4
132. Zheng Y, Hunting DJ, Ayotte P. et al. Radiosensitization of DNA by gold nanoparticles irradiated with high-energy electrons. Radiation Research. 2008;169:19-27
133. Maizel JJV. SDS polyacrylamide gel electrophoresis. Trends in Biochemical Sciences. 2000;25:590-2
134. Stellwagen NC. Electrophoresis of DNA in agarose gels, polyacrylamide gels and in free solution. Electrophoresis. 2009;30:S188-S95
135. Purkayastha S, Milligan JR, Bernhard WA. On the chemical yield of base lesions, strand breaks, and clustered damage generated in plasmid DNA by the direct effect of X rays. Radiation Research. 2007;168:357-66
136. Chen HT, Bhandoola A, Difilippantonio MJ. et al. Response to RAG-Mediated V(D)J Cleavage by NBS1 and γ-H2AX. Science. 2000;290:1962-4
137. Petersen S, Casellas R, Reina-San-Martin B. et al. AID is required to initiate Nbs1/[gamma]-H2AX focus formation and mutations at sites of class switching. Nature. 2001;414:660-5
138. Rogakou EP, Boon C, Redon C. et al. Megabase chromatin domains involved in DNA double-strand breaks in vivo. Journal of Cell Biology. 1999;146:905-15
139. Schultz LB, Chehab NH, Malikzay A. et al. p53 binding protein 1 (53BP1) is an early participant in the cellular response to DNA double-strand breaks. Journal of Cell Biology. 2000;151:1381-90
140. Rappold I, Iwabuchi K, Date T. et al. Tumor suppressor p53 binding protein 1 (53BP1) is involved in DNA damage-signaling pathways. Journal of Cell Biology. 2001;153:613-20
141. Sedelnikova OA, Rogakou EP, Panyutin IG. et al. Quantitative detection of (125) IdU-induced DNA double-strand breaks with gamma-H2AX antibody. Radiation Research. 2002;158:486-92
142. Rothkamm K, Lobrich M. Evidence for a lack of DNA double-strand break repair in human cells exposed to very low x-ray doses. Proceedings of the National Academy of Sciences of the United States of America. 2003;100:5057-62
143. Liu C-J, Wang C-H, Chen S-T. et al. Enhancement of cell radiation sensitivity by pegylated gold nanoparticles. Physics in Medicine and Biology. 2010;55:931-45
144. Ngwa W, Korideck H, Kassis AI. et al. In vitro radiosensitization by gold nanoparticles during continuous low-dose-rate gamma irradiation with I-125 brachytherapy seeds. Nanomedicine: Nanotechnology, Biology and Medicine. 2013;9:25-7
145. Mariotti LG, Pirovano G, Savage KI. et al. Use of the γ-H2AX Assay to Investigate DNA Repair Dynamics Following Multiple Radiation Exposures. PLoS ONE. 2013;8:e79541
146. Hainfeld JF, Dilmanian FA, Slatkin DN. et al. Radiotherapy enhancement with gold nanoparticles. Journal of Pharmacy and Pharmacology. 2008;60:977-85
147. Cho SH. Estimation of tumour dose enhancement due to gold nanoparticles during typical radiation treatments: a preliminary Monte Carlo study. Physics in Medicine and Biology. 2005;50:N163-N73
148. Robar JL. Generation and modelling of megavoltage photon beams for contrast-enhanced radiation therapy. Physics in Medicine and Biology. 2006;51:5487-504
149. McMahon SJ, Mendenhall MH, Jain S. et al. Radiotherapy in the presence of contrast agents: a general figure of merit and its application to gold nanoparticles. Physics in Medicine and Biology. 2008;53:5635-51
150. Kawrakow I, Rogers DWO. The EGSnrc code system: Monte Carlo simulation of electron and photon transport. Ottawa, Canada. 2001
151. Agostinelli S, Allison J, Amako K. et al. GEANT4-a simulation toolkit. Nuclear Instruments and Methods in Physics Research: Section A-Accelerators, Spectrometers, Detectors and Associated Equipment. 2003;506:250-303
152. Jones BL, Krishnan S, Cho SH. Estimation of microscopic dose enhancement factor around gold nanoparticles by Monte Carlo calculations. Medical Physics. 2010;37:3809-16
153. Tsiamas P, Liu B, Cifter F. et al. Impact of beam quality on megavoltage radiotherapy treatment techniques utilizing gold nanoparticles for dose enhancement. Physics in Medicine and Biology. 2013;58:451-64
154. Zygmanski P, Liu B, Tsiamas P. et al. Dependence of Monte Carlo microdosimetric computations on the simulation geometry of gold nanoparticles. Physics in Medicine and Biology. 2013;58:7961-77
155. Cho SH, Jones BL, Krishnan S. The dosimetric feasibility of gold nanoparticle-aided radiation therapy (GNRT) via brachytherapy using low-energy gamma-/x-ray sources. Physics in Medicine and Biology. 2009;54:4889-905
156. Mesbahi A, Jamali F, Garehaghaji N. Effect of Photon Beam Energy, Gold Nanoparticle Size and Concentration on the Dose Enhancement in Radiation Therapy. BioImpacts: BI. 2013;3:29-35
157. Durante M, Loeffler JS. Charged particles in radiation oncology. Nature Reviews Clinical Oncology. 2010;7:37-43
158. Incerti S, Ivanchenko A, Karamitros M. et al. Comparison of GEANT4 very low energy cross section models with experimental data in water. Medical Physics. 2010;37:4692-708
159. Montenegro M, Nahar SN, Pradhan AK. et al. Monte Carlo Simulations and Atomic Calculations for Auger Processes in Biomedical Nanotheranostics. Journal of Physical Chemistry A. 2009;113:12364-9
160. Zhang SX, Gao J, Buchholz TA. et al. Quantifying tumor-selective radiation dose enhancements using gold nanoparticles: a monte carlo simulation study. Biomedical Microdevices. 2009;11:925-33
161. Chow JCL, Leung MKK, Jaffray DA. Monte Carlo simulation on a gold nanoparticle irradiated by electron beams. Physics in Medicine and Biology. 2012;57:3323-31
162. Carter JD, Cheng NN, Qu Y. et al. Nanoscale energy deposition by X-ray absorbing nanostructures. Journal of Physical Chemistry B. 2007;111:11622-5
163. Rajendran L, Knoelker H-J, Simons K. Subcellular targeting strategies for drug design and delivery. Nature Reviews Drug Discovery. 2010;9:29-42
164. Wardlow N, Polin C, Villagomez-Bernabe B. et al. A Simple Model to Quantify Radiolytic Production following Electron Emission from Heavy-Atom Nanoparticles Irradiated in Liquid Suspensions. Radiation Research. 2015;184:518-32
Author biography
Anna Subiel graduated in Biomedical Physics at the University of Gdansk (Poland) in 2009. She was awarded PhD from the University of Strathclyde (UK) in 2014 working on the application of relativistic electron beams from laser-plasma wakefield accelerators as potential radiotherapy sources. This work involved dosimetry and radiobiological studies to test the validity of this approaches. Anna is currently employed as Higher Research Scientist in the Acoustics and Ionising Radiation Group at the National Physical Laboratory in the United Kingdom. Her main research interests involve radiobiology, radiation dosimetry, Monte Carlo modelling for advanced radiotherapy and applications of highly innovative approaches in cancer treatment. Currently Anna is involved in several research activities and collaborative projects including studies on Au nanoparticle-mediated effects in radiation biology and dosimetry, Monte Carlo modelling of radiation detectors and dosimetry of unconventional ultra-short radiation pulses. She is also involved in standardization of dosimetry and quality assurance methods in radiobiological and pre-clinical studies.
Giuseppe Schettino is Principal Research Scientist in the Radiation Dosimetry Group at the UK National Physical Laboratory. His main research interest is in radiation biology, advanced radiotherapy and dosimetry. Current ongoing research activities are focused on dosimetry and radiobiology for MRI-based radiotherapy, biological effectiveness of proton and ion beams, use of gold nanoparticle as radio-sensitizers, definition of new dosimetry quantities closely related to biological response and biological optimization of treatment plans. He is also leading UK initiatives for standardization of dosimetry and QA processes for pre-clinical radiotherapy & radiobiology research. Giuseppe graduated in Nuclear Physics at the University of Naples (Italy) in 1994 and obtained his PhD from King's College London (UK) in 1999, working on the development of ultrasoft X-ray microbeams for radiobiological applications. Following two postdoctoral experiences at the Gray Cancer Institute in the UK (2000-2004) and Center for Radiological Research at the Columbia University in New York (2004-2007), he worked as Lecturer at the Centre for Cancer Research and Cell Biology (CCRCB) of Queen's University Belfast from 2007 to 2013. In 2013, Giuseppe joined the Radiation Dosimetry Group at NPL and he is currently the Knowledge Science Leader for the Acoustic & Ionising Radiation (AIR) Division and honorary senior lecturer at the Queen's University Belfast. To date, he has published over 60 peer-reviewed papers (h-index 24).
![]() Corresponding author: +44 (0)20 8943 8548; anna.subielco.uk; National Physical Laboratory, Hampton Road, Teddington, Middlesex, TW11 0LW, UK.
Corresponding author: +44 (0)20 8943 8548; anna.subielco.uk; National Physical Laboratory, Hampton Road, Teddington, Middlesex, TW11 0LW, UK.
 Global reach, higher impact
Global reach, higher impact