13.3
Impact Factor
Theranostics 2015; 5(11):1275-1290. doi:10.7150/thno.12989 This issue Cite
Research Paper
Zigzag Generalized Lévy Walk: the In Vivo Search Strategy of Immunocytes
1. Britton Chance Center for Biomedical Photonics, Wuhan National Laboratory for Optoelectronics-Huazhong University of Science and Technology, Wuhan 430074, China.
2. MoE Key Laboratory for Biomedical Photonics, Department of Biomedical Engineering, Huazhong University of Science and Technology, Wuhan 430074, China.
3. Cancer Center, Union Hospital, Tongji Medical College, Huazhong University of Science and Technology, Wuhan 430022, China
*H.L. and S.Q. contributed equally to this work.
†L.F. and Q.L. contributed equally to this work.
Received 2015-6-18; Accepted 2015-7-29; Published 2015-9-9
Abstract
Immune responses are based on the coordinated searching behaviors of immunocytes that are aimed at tracking down specific targets. The search efficiency of immunocytes significantly affects the speed of initiation and development of immune responses. Previous studies have shown that not only the intermittent walk but also the zigzag turning preference of immunocytes contributes to the search efficiency. However, among existing models describing immunocytes' search strategy, none has captured both features. Here we propose a zigzag generalized Lévy walk model to describe the search strategy of immunocytes more accurately and comprehensively by considering both the intermittent and the zigzag-turning walk features. Based on the analysis of the searching behaviors of typical immune cell types, dendritic cells and leukocytes, in their native physiological environment, we demonstrate that the model can describe the in vivo search strategy of immunocytes well. Furthermore, by analyzing the search efficiency, we find that this type of search strategy enables immunocytes to capture rare targets in approximately half the time than the previously proposed generalized Lévy walk. This study sheds new light on the fundamental mechanisms that drive the efficient initiation and development of immune responses and in turn may lead to the development of novel therapeutic approaches for diseases ranging from infection to cancer.
Keywords: Search strategy, dendritic cell, leukocyte, amoeboid-manner crawling, zigzag walk, Lévy walk
Introduction
The coordinated searching behaviors of immunocytes for tracking down specific targets constitute the basis of immune responses. For instance, dendritic cells (DCs) scour a sea of mostly normal tissues to capture antigens and then initiate an immune response by processing and presenting antigens [1-3]. Naïve T cells within lymph nodes locate antigen-presenting cells for antigen recognition and are then activated to proliferate and to differentiate into effector cells [1, 4, 5]. Effector T cells scan peripheral tissues to locate target cells bearing the cognate antigen and then contact with them to induce effector functions [6, 7]. Neutrophils scan tissues to locate and clear tissue debris and pathogens [7-9]. Therefore, the search efficiency of immunocytes significantly affects the speed of initiation and development of immune responses [6]. Since targets may be rare and interspersed with other cells within a densely packed natural tissue environment, or may diminish in numbers over the course of an immune response, immunocytes have to devise optimized search strategies [6]. The study of the search strategy may provide new insights regarding the fundamental mechanisms of immune responses and, in turn, may lead to novel therapeutic approaches for diseases ranging from infection to cancer.
The searching behavior of immunocytes is based on their basal movement pattern, an amoeboid-manner crawling [1, 6, 10-13], which eukaryotic cells commonly perform to search for targets that are out of the range of their detection system [14, 15]. We infer from previous studies that the in vivo crawling of immunocytes has two essential features: the intermittent walk and the zigzag turning preference. The intermittent walk is characterized by pause steps between the run steps. Cells performing the zigzag turning preference tend to turn away from their last turn directions and prefer to move forward in a zigzag-manner. Introduced by Mark J. Miller et al. [12] in 2002, the Brownian walk has long been identified as the search strategy of lymphocytes within the lymph nodes [1, 16, 17]. However, in the Brownian walk model, the walker is assumed to move without pauses and turn randomly. Besides, a variety of intermittent random walks [18], such as the Beauchemin model [19, 20], the velocity jump process [21, 22], and the recently discovered generalized Lévy walk (GLW) [23], have been proposed to describe the search strategy of crawling immunocytes. The Lévy walk is a classical search strategy applied for describing foraging patterns in the fields of ecology and evolution and has been observed in a variety of species from microscopic creatures to mammals [24-26] and even humans [25, 27]. In the Lévy walk, the run-step length lrun is distributed according to a power law function with a heavy tail (Lévy distribution):
(1)
where µ is the Lévy exponent with 1 < µ ≤ 3 [17, 25, 28]. Despite controversy [24, 26], it is generally believed that the Lévy walk optimizes the search for sparse targets [25, 28, 29]. The GLW model is a Lévy walk with pauses between runs and the pause time is also drawn from a Lévy distribution. These intermittent walk models make different assumptions for the run and pause steps. Among them, the GLW model is preferred to describe the search strategy that T cells use to capture parasites in the brain. This unexpected search strategy, similar to predators' search for prey, enables T cells to find rare targets more than one order of magnitude more efficiently than Brownian walkers [23]. Moreover, new evidence suggests that naïve T cells in the lymph nodes also use a Lévy search strategy [30]. On the other hand, investigations of the regulation of the pseudopodial extension and the changing of the turn-direction gradually revealed the zigzag turning preference of crawling cells [11, 13-15, 31]. Furthermore, targets are captured 1.6- to 2.4-fold more efficiently by applying the zigzag-turning-based search compared to the random-turning-based search [14].
These studies demonstrate that not only the intermittent walk but also the zigzag turning preference significantly contribute to the search efficiency of crawling cells. Therefore, a model combining these two essential features is urgently needed to more accurately and comprehensively describe the search strategy of immunocytes. Moreover, the feature of GLW-like intermittent walk has only been validated on T cells in the explanted brain [23] and the lymph nodes [30], but on no other immune cell types in their native physiological environment. Regarding DCs in particular, studies merely take them as the targets of T cells and focus on the interactions between T cells and antigen-bearing DCs in the lymph nodes [21, 32, 33]. The search strategy of DCs to locate antigens has not yet been described since DCs are not as motile as T cells. Moreover, although the zigzag turning preference is recognized as a common feature of eukaryotic cells [14], it has only been validated in cultured microglia [10, 13] and neutrophils [11]. Whether immunocytes in their native physiological environment possess this feature also requires further investigation.
To investigate both aspects of the in vivo search strategy of immunocytes and to further incorporate these aspects into a model, we analyzed the searching behaviors of typical immune cell types, DCs and leukocytes (white blood cells, WBCs), in their native physiological environment. The intermittent walk and the zigzag turning preference of immunocytes were observed and quantitatively validated. Thus, we propose a zigzag generalized Lévy walk (Zigzag-GLW) model to involve these two features. We demonstrate that the proposed model can describe the in vivo search strategy of immunocytes well, accounting not only for the intermittent walk, which can be characterized by the GLW, but also for the zigzag turning preference. Furthermore, we studied the search efficiency of immunocytes and found that the zigzag crawling enables immunocytes to capture rare targets in approximately half the time than GLW walkers. These findings shed new light on the fundamental mechanisms driving the efficient initiation and development of immune responses.
Materials and Methods
Mice
CD11c-EYFP (strain name: B6.Cg-Tg(Itagx-Venus)1Mnz/J) mice were purchased from Jackson Laboratory (Bar Harbor, Maine, USA). B6-EGFP (strain name: C57BL/6-Tg(CAG-EGFP)1Osb/J) mice were obtained from Dr. Zhiying He (Second Military Medical University, Shanghai, China). All mice used in the present study were 10-12 weeks old. These transgenic mice were reproduced in the specific-pathogen-free animal facility of Britton Chance Center for Biomedical Photonics, Wuhan National Laboratory for Optoelectronics-Huazhong University of Science and Technology (Wuhan, Hubei, China). All mouse experiments were performed in compliance with protocols that had been approved by the Hubei Provincial Animal Care and Use Committee and with the animal experimental guidelines of the Animal Experimentation Ethics Committee of Huazhong University of Science and Technology (Wuhan, Hubei, China). In CD11c-EYFP mice, DCs were labeled with Venus fluorescent protein. In B6-EGFP mice, all cells expressed enhanced green fluorescent protein (EGFP), while WBCs were identified based on their size and shape described in previous studies [12, 34, 35].
Intravital microscopic imaging
To determine the behaviors of immunocytes in their native physiological environment, DCs and WBCs within the skin were tracked in vivo using a dorsal skinfold window chamber (APJ Trading, Ventura, California, USA) surgically implanted into the mice (Additional File 6: Fig. S1), as described by Gregory M. Palmer et al. [36]. For the chamber, a titanium frame was used to support the transparent window. The dorsal skin of the mouse was folded up into the frame and one side of the skin was removed in a circular region of ~1 cm in diameter. Afterwards, the superficial fascia of the other side of the skin was removed, to allow for the observation of immunocytes in the dermis, which is richer of various immunocytes than other skin layers. Furthermore, a round cover slip was placed over the opening for high-resolution microscopic imaging (Additional File 6: Fig. S1). To relieve the inflammation and pain caused by surgery, Tolfedine (16.25 mg kg-1; Vétoquinol, Québec, Canada) was administered to the mice by intraperitoneal injection immediately after the implantation.
Three days later, intravital imaging was performed on an A1R MP+ confocal microscope (Nikon, Tokyo, Japan). The mice were anesthetized by inhalation of 0.5-1.5% isoflurane in oxygen flow using a Matrx VMS small animal anesthesia machine (Midmark, Dayton, Ohio, USA). During imaging, the temperature of the mice was monitored and maintained at 37 °C. Venus and EGFP were excited by an Ar+ laser at 514 nm and 488 nm, respectively, and corresponding emission signals of 500-550 nm were separately detected. Three-dimensional (x, y, time) imaging was carried out using a 20×/0.75NA objective (Nikon, Tokyo, Japan) with a 10 s interval for 10-20 min, which was the typical time length during which most cells didn't migrate out of the field of view. The depth of the imaging plane ranges from the interface between the superficial fascia and dermis to ~50 μm under the interface (Additional File 6: Fig. S1).
Cell tracking
Based on the movies, cells were tracked using Image-Pro Plus (Media Cybernetics, Bethesda, Maryland, USA). Each cell trajectory consisted of a sequence of centroid coordinates (x(τ), y(τ)) of the cell's contours, where the time τ = n⊿t (⊿t is the time interval between adjacent time-lapse images and n = 1, 2, 3…). A displacement between any two cell locations was defined as r(t) = [(x(τ + t) - x(τ))2 + (y(τ + t) - y(τ))2]1/2, where the time interval t = n⊿t (n = 1, 2, 3…) [37]. A cell's instantaneous velocities were then calculated as V = r(τ, τ +⊿t) /⊿t, where r(τ, τ +⊿t) is the displacement between time τ and τ +⊿t. The mean velocity of a cell was calculated as Vmean = 〈V〉.
Recognition of turns
To analyze the turning characteristics of immunocytes, the turns of each cell trajectory have to be recognized (Additional File 6: Fig. S2A). Here, we applied the method proposed by Liang Li et al. [14]. First, cell trajectories were smoothed by a moving average over three consecutive locations. Changes in directions of consecutive displacements r(⊿t) were then calculated and denoted as ⊿φ (Additional File 6: Fig. S2B). Afterwards, locations with ⊿φ values going above a certain threshold were marked. For each trajectory, the threshold value was chosen as the mean value of ⊿φ of the given trajectory. The marked locations were then filtered by restricting the minimum time interval and the minimum distance interval between any two adjacent turns to 0.5 min and 1 µm, respectively. Finally, only the remaining marked locations were identified as turns (Additional File 6: Fig. S2A). Trajectories that covered a time length less than 5 min were excluded from analysis because they contained too few turns that might lead to a biased quantitative characterization of the immunocytes' turning preference. A turn with a positive turn angle was recorded as a left turn (counterclockwise), otherwise it was recorded as a right turn (clockwise) (Additional File 6: Fig. S2A).
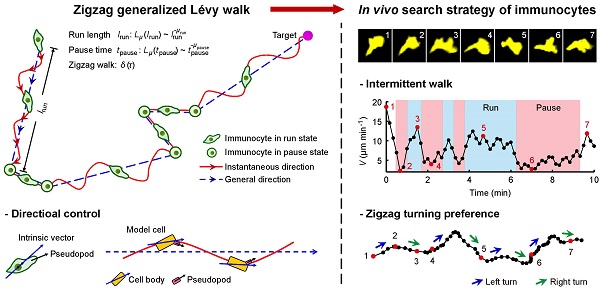
Schematic diagram of the immunocytes' search strategy. (A) The zigzag generalized Lévy walk (Zigzag-GLW) proposed to describe the strategy of immunocytes to search for a target. The Zigzag-GLW trajectory consists of alternating run and pause states. The run length lrun of each run step and the pause time tpause of each pause step are all drawn randomly from Lévy distributions Lμ. The run step is either a zigzag-manner, long directional persistence (i.e., the first run step) or a straight-line, short migration (i.e., the second run step). In the zigzag walk, the instantaneous directions (the red solid arrow) of the immunocyte are summed up to the general direction (blue dashed arrow) and exhibit stochastic oscillations around that direction. (B) The general direction of each run step is assumed to be fixed by the immunocyte's intrinsic polarity (blue solid arrow, possibly a vector directed from the center of nucleus to the position of the centrosome). Pseudopods (black arrow) swing back and forth about the internal vector, which possibly leads to the immunocyte's oscillating migration along the general direction. A cartoon model cell was drawn to describe the directional control [14, 38]. (C) A colored noise δ(τ) was used after coordinate transformation to simulate the zigzag walk. τ0 and trun are the start time and the duration of a given run step, respectively.
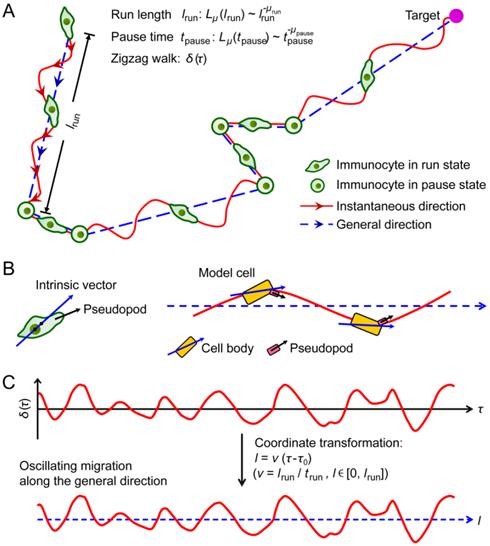
Model
A Zigzag-GLW model was proposed to describe the search strategy of immunocytes (Fig. 1). In this model, alternating states of run and pause form the migration trajectory of the walker. In the run state, the walker moves for a displacement lrun, whereas in the pause state, the walker remains stationary for a time tpause. lrun and tpause are drawn randomly from Lévy distributions with Lévy exponents μrun and μpause, respectively. During a run step persisting shorter than the time Tl, the walker moves along a straight line, otherwise it migrates in a zigzag manner around a general direction (Fig. 1A). Tl is defined as the shortest persistent time that a walker moves with an approximately consistent velocity along a straight line that, is assumed to be too short for an immunocyte to make a turn. The general direction of each run step is fixed by the immunocyte's intrinsic polarity. In this model, the general direction is randomly selected, reflecting the fact that the immunocytes have no preferred moving direction when the target is out of the range of the immunocyte's detection system. The instantaneous directions during the zigzag walk are summed up to the general direction and exhibit noisy oscillations around that direction in molding. In this way, the stochastic oscillating migration, which is determined by pseudopodial extension of immunocytes, was modeled (Fig. 1B) [14, 38]. During running, the straight-line velocity is fixed and along the general direction. It is defined as v = lrun / trun, where trun is the duration of a given run step. Thus, in a zigzag run step, while immunocytes progress during a certain time interval about a defined distance in the general direction, the path lengths they cover along trajectories in their instantaneous directions can vary (Fig. 1C). Consequently, we modeled the fluctuation of instantaneous velocities of immunocytes during zigzag migration.
To simulate the model, lrun and tpause (in simulation units, distance l0 or time t0) were generated by calculating Lévy-distributed random variables [23, 39] with μrun and μpause, respectively. The scale factors of the Lévy distributions were set to one (in simulation units, l0 or t0). The instantaneous directions of the zigzag walk exhibit stochastic oscillations around the general direction and were modeled by a colored noise in the previous study [14]. Similarly, a colored noise δ(τ) describing the stationary stochastic process was involved here [40].
(2)
where w(τ) is a zero-mean Gaussian white noise with the variance σ2. δ(τ) was coordinate transformed to δ(l / v + τ0) (in µm) by l = v (τ - τ0) to simply simulate the zigzag walk in run steps persisting longer than Tl. l is the distance that the immunocyte covers along the general direction from the starting point of a given run step, and τ0 is the start time of the run step (Fig. 1C). Since w(τ) is the driving source of δ(τ), the swinging amplitude of the zigzag migration can be determined by σ2 when pi and qj are given. In addition, the frequency of zigzag-turn occurring can be adjusted by resampling δ(l / v + τ0) to δ(f(l / v + τ0)) (for f > 1, the frequency increases, whereas it decreases for f < 1). Thus, in the run state, the simulated walker randomly chooses a general direction and moves forward for a displacement lrun, in a zigzag manner for trun longer than Tl or along a straight line for trun shorter than Tl. During the zigzag walk, the walker executes oscillating migration described by δ(f(l / v + τ0)) along the general direction. In the pause state, the walker remains stationary for tpause.
To fit the Zigzag-GLW model to the experimental data, the simulation units must be mapped onto experimental units first. Here, we set t0 =⊿t / 20 and l0 = v t0 to ensure good statistics. Next, µrun, µpause, v, and δ(τ) have to be determined. Important parameters of the Zigzag-GLW model that need to be estimated are summarized in Table 1.
Important parameters of the zigzag generalized Lévy walk model.
| Symbol | Description |
|---|---|
| μrun | Lévy exponent of the Lévy distribution of the run step's displacement lrun |
| μpause | Lévy exponent of the Lévy distribution of the pause step's pause time tpause |
| v | Straight-line velocity of each run step, v = lrun / trun, where lrun and trun are the displacement and duration of a given run step, respectively |
| σ2 | Variance of the zero-mean Gaussian white noise w(τ) and determines the swinging amplitude of the zigzag walk |
| f | Coefficient used to resample colored noise δ(τ) to δ(fτ) to adjust the frequency of zigzag-turn occurring |
We first used a GLW parameter estimation method (refer to Additional File 6: Supplementary Methods and Discussion and Additional File 6: Figs. S3-S5) to determine µpause and approximate values of µrun and v. The zigzag walk is irrelevant to pause steps but relative to the run steps persisting longer than Tl. Therefore, we were able to remain µpause constant while simply adjusting µrun and v and to evaluate the best value for δ(τ) to fit the experimental data. Tl was estimated as 0.5-2 times of the immunocytes' diameter over their maximum instantaneous velocity. In δ(τ), either set of variables pi and qj or σ2 and f can determine the amplitude and frequency of the model zigzag migration. To estimate δ(τ), we set pi and qj to specific, constant values while determine the approximate values of σ2 and f with respect to the amplitude and frequency of the experimental zigzag migration. Alternatively, σ2 and f can be set constant (f = 1) while evaluating a series of values for pi and qj to fit the experimental zigzag migration optimally. However, the latter method is not preferred since it complicates the fitting process by involving too many unknown parameters. After the above estimation, µpause and approximate values for µrun, v, σ2, and f were determined. The displacement probability density distribution p(r(t)) and the turn-direction autocorrelation Corr(k) are representatives of displacement statistics and turning statistics, respectively.
(3)
where 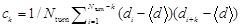 , Nturn is the number of turns in a given cell trajectory, k = 0, 1, 2…, d = θ / |θ|, and θ is the turn angle [13, 14, 41, 42]. Thus, in order to select a precise combination, we finally used the least square fitting to determine the best values for µrun, v, σ2, and f by minimizing the difference between model p(r(t)) and experimental p(r(t)) as well as minimizing the difference between model Corr(k) and experimental Corr(k).
, Nturn is the number of turns in a given cell trajectory, k = 0, 1, 2…, d = θ / |θ|, and θ is the turn angle [13, 14, 41, 42]. Thus, in order to select a precise combination, we finally used the least square fitting to determine the best values for µrun, v, σ2, and f by minimizing the difference between model p(r(t)) and experimental p(r(t)) as well as minimizing the difference between model Corr(k) and experimental Corr(k).
Evaluation of model-fitting quality
To evaluate the model-fitting quality, the Akaike information criterion (AIC) was applied. It quantifies the amount of evidence for a given model, hence provides a quantitative measure for model selection. It accounts for both the goodness of fit and the complexity (number of parameters) of a given model. The Akaike weight calculated using AIC equals the relative probability of a given model to be the most accurate of all tested models [43]. To select a model that can capture both the intermittent-walk characteristics and the turning preference of immunocytes, we calculated Akaike weights using AIC for least square fitting [43] based on not only p(r(t)) but also Corr(k).
Immunofluorescence histological analysis
To reveal the cell types of the identified EGFP cells in B6-EGFP mice and to validate whether these cells were WBCs, immunofluorescence histological analysis was performed. After the same sample preparation as used for intravital imaging, skin tissues from the site of the dorsal skinfold window chamber were excised and fixed in 4% paraformaldehyde for 24-48 h at 4 °C. The tissues were then embedded in optimal cutting temperature (OCT) compound (Tissu-Tek; Sakura Finetek USA, Inc., Torrance, California, USA) and frozen at -20 °C. 10-μm-thick sections of embedded tissues were cut and air-dried afterwards. OCT compound was removed by washing three times in phosphate buffered saline, and then the tissues were immunostained with CD3-Alexa Fluor 594 (17A2), Ly6G-Alexa Fluor 700 (1A8), and F4/80-Alexa Fluor 647 (BM8) (Biolegend, San Diego, California, USA) to label T cells, neutrophils, and macrophages, respectively. Finally, the tissue sections were imaged using a confocal microscope (LSM 710; Carl Zeiss Microscopy GmbH, Hamburg, Germany). Based on the obtained images, the numbers of identified EGFP cells and various types of immunocytes labeled with different immunofluorescences were counted, respectively. Then, the ratios of the number of each immunocyte type over that of the identified EGFP cells were calculated, respectively.
Statistical analysis and programming
Statistical analyses were performed with GraphPad Prism (GraphPad Software, San Diego, California, USA). For the comparison of two groups, the two-tailed unpaired t test was used, whereas for the comparison of three groups or more, the one-way ANOVA followed by the Tukey's multiple comparison test was used. Differences were considered to be statistically significant for P < 0.05. Other analyses and original programming were carried out using MATLAB (MathWorks, Natick, Massachusetts, USA).
Results
Amoeboid-manner crawling
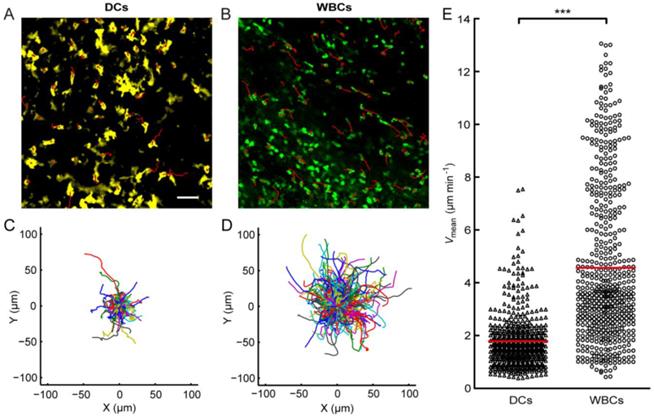
To study the in vivo search strategy of immunocytes, we observed the searching behaviors of the typical immune cell types, DCs and WBCs, in their native physiological environment. Here, we focused on skin tissues. Searching generally occurs when the target is out of the range of its searcher's detection system. Therefore, we didn't specifically involve any external stimulation into the mice, to ensure that the skin tissues we focused on contain only negligible amounts of targets, so that the targets are out of the range of most immunocytes' detection systems. In this case, some DCs randomly extend and retract their dendrites, and some DCs constitutively migrate throughout the skin tissues, to detect danger-associated antigens [6, 44-46]. Meanwhile, WBCs patrol the skin tissues to encounter their targets to exert immune effects [6]. These behaviors, described in previous studies, are consistent with our observations (Fig. 2 and Additional File 1: Movie S1 and Additional File 2: Movie S2). DCs confined within a small area, with dendrites randomly extending and retracting, were interspersed with some actively migrating ones. Their mean velocity Vmean was 1.78 ± 1.02 µm min-1 (mean ± SD) (Fig. 2A, 2C, and 2E and Movie S1). WBCs were actively migrating with a Vmean of 4.56 ± 2.94 µm min-1 (mean ± SD) (Fig. 2B, 2D, and 2E and Movie S2).
Motility of dendritic cells (DCs; A, C) and leukocytes (white blood cells, WBCs; B, D) migrating in vivo. (A, B) Overlay of fluorescence images of DCs (A) and WBCs (B) with their trajectories (red solid lines). Scale bar: 50 µm. (C, D) Trajectories superimposed after normalizing their start points to the origin. (E) Mean velocities Vmean of DCs (triangles) and WBCs (circles). Vmean values of DCs were significantly lower than those of WBCs (***: P < 0.001, two-tailed unpaired t test). The red solid line indicates the mean of Vmean values of all cells. The data were obtained from three independent experiments with 1-2 mice per group for each experiment (DCs: 9 movies, 588 cells; WBCs: 7 movies, 570 cells).
Crawling patterns of dendritic cells (DCs; A, C, and E) and leukocytes (while blood cells, WBCs; B, D, and F). (A, B) Fluorescence images recorded at the indicated time points 1-7, as defined in C and D (scale bars: 10 µm). (C, D) Instantaneous cell velocities V determined over 10 min in 10 s intervals. Large instantaneous velocities are assigned to run states (light blue) and small instantaneous velocities to pause states (pink). (E, F) Cell trajectories recorded by time-lapse imaging (scale bars: 10 µm). Left turns and right turns are indicated by blue and green arrowheads, respectively. Black and red dots correspond to time points with 10 s intervals of the cells' movement as defined in C and D.
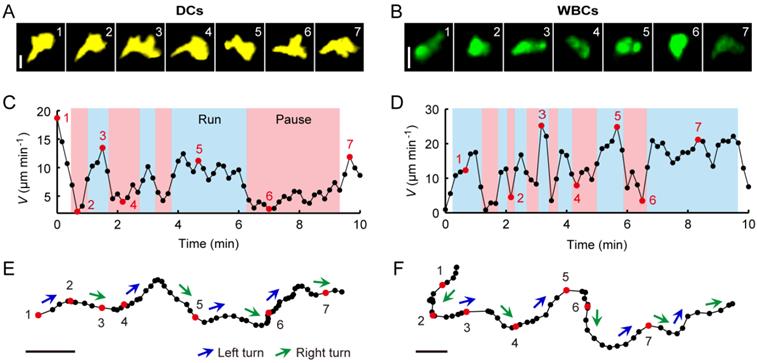
Furthermore, we analyzed the basal movement patterns of these two cell types, which present the foundation of their search strategy. We found that based on extension and retraction of pseudopods (Fig. 3A and 3B), the cells typically crawled forward in an amoeboid manner (Additional File 3: Movie S3 and Additional File 4: Movie S4) with two essential features (Fig. 3C-3F). On the one hand, according to the variation of the cells' instantaneous velocity over time, we found that the cells showed a signature of intermittent walk (Fig. 3C and 3D). On the other hand, by analyzing the order in which left turns and right turns appeared within the sequence of cell turning, the cells were found to show the zigzag turning preference (Fig. 3E and 3F). Thus, both features, the intermittent walk and the zigzag turning preference, were observed in DCs and WBCs.
To describe the search strategy of immunocytes more accurately and comprehensively, we quantitatively analyzed the search strategy of immunocytes base on the two crawling features and proposed a Zigzag-GLW model to involve them. In the proposed model, the intermittent-walk characteristics, the zigzag turning preference, the variation characteristics of instantaneous velocities, as well as the general and instantaneous directional control of immunocytes were taken into consideration. The details of this model are described in Materials and Methods and Fig. 1.
GLW-like intermittent walk
To analyze the intermittent walk quantitatively and to provide more constraints for fitting the model of the immunocytes' search strategy, we considered a series of displacement statistics since deriving precise run length and pause time of the intermittent walk from the experimental data is almost impossible. These displacement statistics included the P(r(t)) as a function of t; a displacement scale factor ζ(t), used to collapse P(r(t)) at different t values onto a single curve; a normalized displacement correlation as a function of τ
(4)
where r(τ, τ + t) is the displacement between the time τ and τ + t; and the classical mean squared displacement m.s.d. [23].
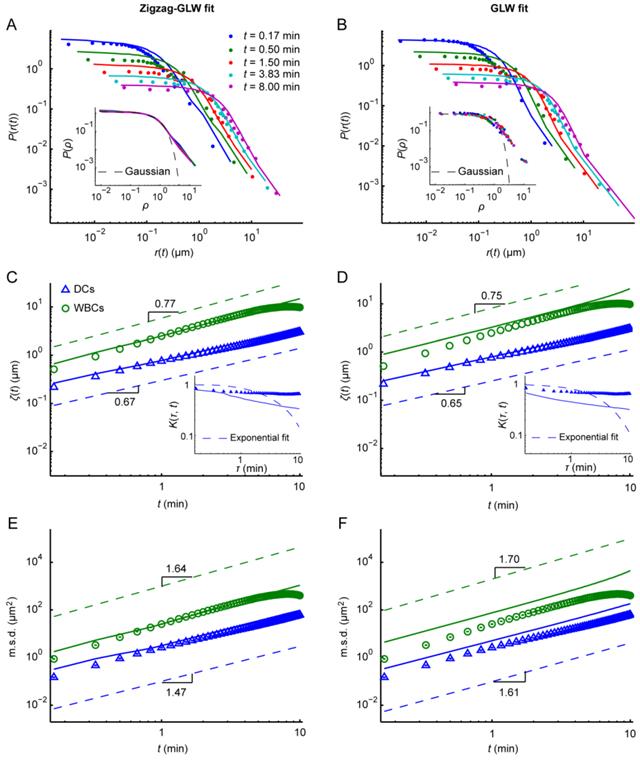
For DCs and WBCs, the P(r(t)) was scale free and had a heavier tail than the Gaussian distribution (Fig. 4A, the inset of Fig. 4B, Additional File 6: Fig. S6A, and the inset of Additional File 6: Fig. S6B) and the K(τ,t) decayed more slowly than exponentially (the inset of Fig. 4C). These findings indicate that immunocytes might execute a GLW-like intermittent walk. To validate this assumption, the GLW model was fitted to the experimental data. The results showed that the GLW model fits the data of DCs and WBCs well regarding the displacement statistics (Figs. 4B, 4D, 4F, and S6B), which validates the GLW-like intermittent walk of immunocytes.
To validate further whether the Zigzag-GLW model has captured the feature of GLW-like intermittent walk, the Zigzag-GLW fitting of the experimental data (Figs. 4A, 4C, 4E, and S6A) was compared with the corresponding GLW fitting (Figs. 4B, 4D, 4F, and S6B). The estimates of important model parameters are listed in Table 2. In general, the displacement statistics of DCs and WBCs were strongly consistent with the Zigzag-GLW model. Moreover, the parameters P(r(t)) and K(τ,t) of the Zigzag-GLW model (Figs. 4A and S6A and the inset of Fig. 4C) showed similar characteristics to the GLW model (Figs. 4B and S6B and the inset of Fig. 4D). Furthermore, the values γ ≈ 0.67 and 0.77 in ζ(t) ~ tγ resulting from the Zigzag-GLW fitting for DCs and WBCs, respectively (Fig. 4C), were very similar to the corresponding values obtained from the GLW fitting (γ ≈ 0.65 and 0.75, respectively; Fig. 4D). The values α ≈ 1.47 and 1.64 in m.s.d. ~ tα resulting from the Zigzag-GLW fitting for DCs and WBCs, respectively (Fig. 4E), were also very similar to those values resulting from the GLW fitting (α ≈ 1.61 and 1.70, respectively; Fig. 4F). These results demonstrate that the GLW-like intermittent walk of immunocytes has been captured by the Zigzag-GLW model.
Displacement statistics of dendritic cells (DCs) and leukocytes (white blood cells, WBCs) compared with the respective zigzag generalized Lévy walk (Zigzag-GLW) fittings (A, C, and E) and generalized Lévy walk (GLW) fittings (B, D, and F). (A, B) Displacement probability density distributions P(r(t)) of DCs at different time intervals t. Colored dots indicate the experimental data. Solid lines indicate the model fittings. The insets show P(r(t)) at different t after normalizing the displacement r(t) by the scale factor ζ(t) (ρ = r(t) / ζ(t)). Normalized P(r(t)) in the insets of A and B were obtained from the Zigzag-GLW fitting and the experimental data, respectively. The Gaussian fittings of the normalized P(r(t)) at t = 5 min are indicated by dashed lines for comparison. (C, D) Displacement scale factors ζ(t) of DCs (triangles) and WBCs (circles) with the respective model fittings (solid lines). ζ(t) increased approximately according to a power law tγ, where γ ≈ 0.67 and 0.77 in the Zigzag-GLW fittings for DCs and WBCs, respectively (C), and 0.65 and 0.75 in the corresponding GLW fittings (D) (dashed lines). The insets show the normalized displacement correlation K(t,t) of DCs (triangles) with the corresponding model fittings (solid lines). K(t,t) decayed more slowly than exponentially (dashed lines) over time τ. (E, F) Mean squared displacements m.s.d. of DCs (triangles) and WBCs (circles) with the respective model fittings (solid lines). m.s.d. grew approximately according to tα, where α ≈ 1.47 and 1.64 in the Zigzag-GLW fittings for DCs and WBCs, respectively (E), and 1.61 and 1.70 in the corresponding GLW fittings (F) (dashed lines). The error bars for K(τ,t) and m.s.d. denote the SEM.
Fitting the zigzag generalized Lévy walk (Zigzag-GLW) model and the generalized Lévy walk (GLW) model to the data of dendritic cells (DCs) and leukocytes (white blood cells, WBCs). Exp: experimental data. Model fit: results of the model fitting.
| Model | Estimated model parameters | Vmean (mean ± s.t.d.) (μm min-1) | ||||||
|---|---|---|---|---|---|---|---|---|
| μrun | μpause | v (μm min-1) | σ2 (μm2) | f | Exp | Model fit | ||
| DCs | Zigzag-GLW | 2.35 | 2.10 | 6.63 | 0.3 | 2 | 1.78 ± 1.02 | 1.81 ± 0.84 |
| GLW | 2.50 | 2.10 | 22.89 | - | - | 1.91 ± 0.76 | ||
| WBCs | Zigzag-GLW | 2.15 | 2.90 | 9.64 | 0.3 | 2 | 4.56 ± 2.94 | 6.23 ± 1.48 |
| GLW | 2.40 | 2.90 | 43.37 | - | - | 8.21 ± 2.49 | ||
In addition, the approximate µrun values obtained from the model fitting of DCs and WBCs (Table 2), indicate that the cells' run-length distributions are nearly the same; however, obvious gaps in µpause and v values (Table 2) reflect significantly different pause-time distributions and running velocities of the two cell types. This is consistent with the migration characteristics of the two types of immunocytes described above (Figs. 2 and 3). Notably, within a given run step, a Zigzag-GLW walker might migrate along a zigzag path, whereas a GLW walker migrates along a straight line. Therefore, the values of the straight-line velocity v (Table 1) of the Zigzag-GLW model and that of the GLW model are incomparable, whereas the values of the mean velocity Vmean are comparable. Fitting revealed that, the Vmean values of these two models are similar to each other and, furthermore, similar to those of the experimental data (Table 2).
Zigzag turning preference
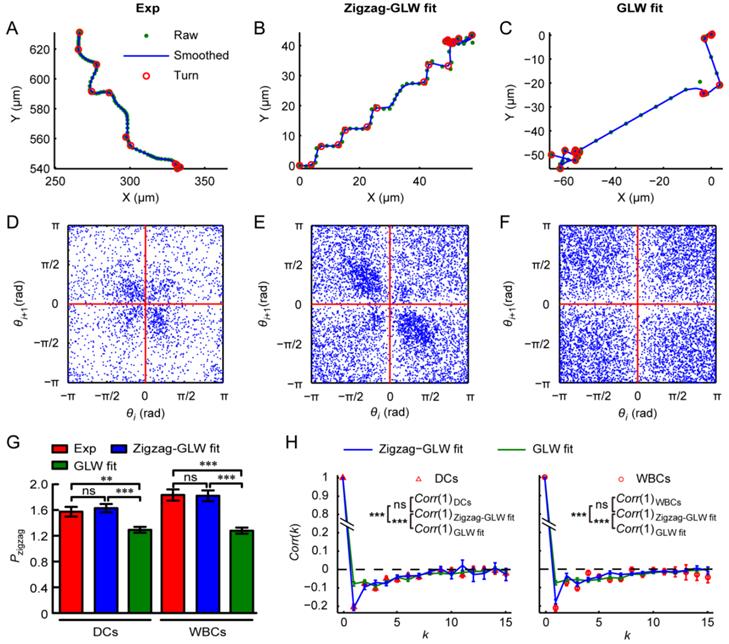
By recognizing turns within cell trajectories, DCs and WBCs were found to migrate in a zigzag manner for long directional persistence (typical trajectories are shown in Fig. 5A and Additional File 6: Fig. S7A, the recognized turns are marked by red circles), which is consistent with our previous observations (Fig. 3E and 3F). To quantify the turning characteristics of immunocytes further, we analyzed the return map of turn angles, the zigzag preference index Pzigzag, and Corr (k) (Equation 3) [13, 14, 41, 42]. The return map is a scatterplot that takes the ith turn angle θi of a specific cell trajectory as its x coordinate and the adjacent downstream turn angle θi+1 as its y coordinate.
(5)
where Nright-left is the total number of cases in which a right turn is followed by a left turn in a given cell trajectory; for Nleft-right, Nleft-left, and Nright-right, the definitions are analogous.
For DCs and WBCs, the number of data points in the second (right-left turns) and fourth (left-right turns) quadrants of the return map was obviously larger than that in the first (left-left turns) and third (right-right turns) quadrants (Figs. 5D and S7D), indicating that the immunocytes tend to turn away from their last turn directions. The clustering of the data points in the return map (Figs. 5D and S7D) indicates that the distribution of turn amplitudes is not uniform. Furthermore, Pzigzag was found to be obviously larger than one (Fig. 5G), indicating a significantly higher probability for an immunocyte to turn away from its last turn direction than to turn following that last turn direction. A visible anticorrelation between adjacent turn directions (Corr(1); Fig. 5H) also demonstrates that an immunocyte prefers to move along a direction opposite to its last or next turn. These findings robustly verify the zigzag turning preference of immunocytes.
To validate whether the Zigzag-GLW model has captured the feature of zigzag turning preference, the trajectories and turning statistics resulting from the Zigzag-GLW fitting (Figs. 5B, 5E, 5G-5H, S7B, and S7E and Table 2) were compared with those of the experimental data (Figs. 5A, 5D, 5G-5H, S7A, and S7D). The Zigzag-GLW trajectories (Figs. 5B and S7B) were found to be similar to the DC and WBC trajectories (Figs. 5A and S7A). Furthermore, the Zigzag-GLW model fits the experimental data well regarding the turning statistics (the return map of turn angles (Figs. 5D, 5E, S7D, and S7E), Pzigzag (Fig. 5G) and Corr(k) (Fig. 5H)). This shows that the Zigzag-GLW model has captured the feature of zigzag turning preference of immunocytes. In addition, the zigzag walk of DCs and WBCs was described in the Zigzag-GLW fitting by the same colored noise δ(fτ) (Tl = 0.5 min, Np = 3, p1 = 1.5, p2 = -0.7, p3 = -0.1, Nq = 2, q1 = 0.5, q2 = 0.2; other parameters are listed in Table 2). This indicates that the zigzag crawling patterns of these two types of immunocytes are nearly the same, which is consistent with our previous observations (Fig. 3, Movies S1-S4).
Moreover, since the GLW model can describe the immunocytes' intermittent walk well, the GLW trajectories and turning statistics were analyzed to examine the GLW model's ability to describe the immunocytes' turning characteristics. In GLW trajectories, the path of directional persistence was found to be rather straight than zigzag (Figs. 5C and S7C). For the GLW fitting of the experimental data (Figs. 5C, 5F, 5G-5H, S7C, and S7F and Table 2), the data points were uniformly distributed in the return map (Figs. 5F and S7F), indicating that the adjacent turn directions are uncorrelated. Thresholding in the turn-detection algorithm and coarse graining in the angle calculation caused the sparse distribution of data points within the area near the coordinate axes (red solid lines in Figs. 5F and S7F) [14]. Pzigzag was approximately one (Fig. 5G) and the anticorrelation between adjacent turn directions was negligibly weak (Corr(1); Fig. 5H). These data indicate that no special turning preference exists in the GLW, which results from the random orientation of each GLW run step [23]. These results demonstrate that although the displacement statistics of DCs and WBCs exhibit a GLW signature (Fig. 4B, 4D, and 4F), the zigzag turning preference of immunocytes is not captured by the GLW model.
Since the Zigzag-GLW model involves more parameters than the GLW model, the Akaike weight was calculated to evaluate the model-fitting quality of these two models, accounting for both the goodness of fit and the complexity (number of parameters) of a given model. Regarding the intermittent-walk characteristics, the Akaike weights showed that the Zigzag-GLW model and the GLW model were almost on a par (Table 3). However, regarding the turning preference, the Akaike weights indicated that the Zigzag-GLW model is superior to the GLW model (Table 3). These results are consistent with the conclusions of the above analysis (Figs. 4 and 5). Concluding, the statistical analysis and the model fitting demonstrate that immunocytes execute the Zigzag-GLW search strategy in vivo, which is characterized by the GLW-like intermittent walk and the zigzag turning preference.
Turning characteristics of dendritic cells (DCs; Exp) and leukocytes (white blood cells, WBCs; Exp) compared with the respective zigzag generalized Lévy walk (Zigzag-GLW) fittings and generalized Lévy walk (GLW) fittings. (A-C) Typical migration trajectories of WBCs (A) and the corresponding Zigzag-GLW fitting (B) and GLW-fitting (C) (green dots: raw trajectories (Raw); blue solid lines: smoothed trajectories (Smoothed); red circles: recognized turns (Turn)). (D-F) Return maps of turn angles θ of WBCs (D) and the corresponding Zigzag-GLW fitting (E) and GLW-fitting (F). i denotes the sequence number of θ within each trajectory. (G, H) Comparison of zigzag preference indexes Pzigzag (G) and autocorrelations of turn directions Corr(k) (H) of DCs and WBCs with the corresponding model fittings. k denotes the turn lag. ns: no significant difference; **: 0.001 <P < 0.01; ***: P < 0.001, one-way ANOVA and Tukey's multiple comparison test. The error bars denote the SEM.
Akaike weights calculated from the data of dendritic cells (DCs) and leukocytes (white blood cells, WBCs). Zigzag-GLW: zigzag generalized Lévy walk. GLW: generalized Lévy walk.
| Model | Akaike weight | |||
|---|---|---|---|---|
| Intermittent-walk characteristics | Turning preference | |||
| DCs | WBCs | DCs | WBCs | |
| Zigzag-GLW | 0.3793 | 1 | 1 | 1 |
| GLW | 1 | 0.5290 | 0.0046 | 0.0024 |
Zigzag crawling pattern enables immunocytes to capture rare targets in shorter time
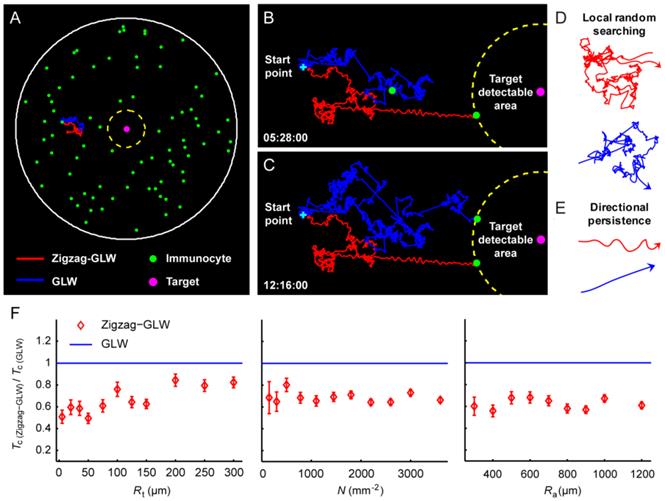
To investigate how the Zigzag-GLW search strategy of immunocytes affects the speed of initiation and development of immune responses, we analyzed the search trajectory and search efficiency of immunocytes using a search-and-capture model [23]. In this model, immunocytes (green) with a density N are placed in a search area of radius Ra to search for a target of a detectable radius Rt (yellow boundary) at the center (Fig. 6A and Additional File 6: Supplementary Methods and Discussion). With the aim to reveal the role of the immunocytes' zigzag crawling pattern in immune responses, we compared the Zigzag-GLW and the GLW with approximate Vmean values regarding the search trajectory and search efficiency.
By comparing typical search trajectories (Fig. 6B and 6C and Additional File 5: Movie S5), we found that the Zigzag-GLW trajectory contained less local random searching (Fig. 6D) but more directional persistence (Fig. 6E) than the GLW trajectory. Thus, executing the Zigzag-GLW enables immunocytes to avoid oversampling within a small local area and to step into a new environment. Moreover, by performing persistent, zigzag directional movement according to the Zigzag-GLW rather than the straight-line running according to the GLW (Fig. 6E), immunocytes encounter more cells and molecules, which improves the chance of finding a target. Furthermore, by investigating the search efficiency over a series of values of Rt, Ra, and N (Additional File 6: Supplementary Methods and Discussion), we found that immunocytes executing the Zigzag-GLW capture their target in approximately half the time, compared with immunocytes executing the GLW (capture time Tc; Fig. 6F). This arises from the larger territory covered by the Zigzag-GLW relative to the GLW in a given time frame, which may be caused by the different characteristics of these two models' search trajectories described above (Fig. 6B-6E).
Besides, we calculated the conventional search efficiency η, which is defined as the inverse of the sum of the path lengths of all immunocytes at the instant when an immunocyte first reaches the target [29]. As shown in Additional File 6: Fig. S8, the η values of the Zigzag-GLW and the GLW are similar. This result indicates that the zigzag crawling pattern has no significant effect on the search efficiency of an immunocyte in close proximity to its target since the value Tc is largely determined by the initial distance between the immunocyte and the target, and the value η is determined by the shortest Tc (according to its definition). Nevertheless, the more immunocytes capture extremely rare targets, the more conducive they will be to the initiation and development of immune responses. Thus, Tc might be a more important indicator of the immunocytes' search efficiency than η.
These results demonstrate that the Zigzag-GLW search strategy improves the immunocytes' search efficiency by shortening the capture time Tc. Thus, the zigzag crawling pattern of immunocytes might be one of the driving factors for the efficient initiation and development of immune responses.
Discussion
Cell types of the investigated WBCs
In-situ immunofluorescence histological analysis reveals that, among the identified EGFP cells in B6-EGFP mice, T cells accounted for ~31%, neutrophils accounted for ~51%, whereas the number of macrophages was too small to be detectable (Additional File 6: Fig. S9). According to previous studies [7, 47], this result demonstrates that the identified cells were surely WBCs, but the number of neutrophils has increased compared with that in the normal skin. This is because that the surgical injury involved by the implantation of dorsal skinfold window chamber leaded to inflammation, although we didn't specifically involve any external stimulation into the mice. In order to ensure that the targets for the immunocytes are rare to allow the study of immunocytes' search strategy, we used Tolfedine to relieve the inflammation caused by surgery and performed the intravital microscopic imaging three days after chamber implantation to avoid the peak hour of inflammation response [48].
Comparison of the search trajectories and search efficiencies of the zigzag generalized Lévy walk (Zigzag-GLW) with the generalized Lévy walk (GLW). (A) The search-and-capture model: immunocytes (green) with a density N are placed in a search area of radius Ra (white solid boundary) to search for a target (magenta) of a detectable radius Rt (yellow dashed boundary) at the center by performing the Zigzag-GLW (red) or the GLW (blue). (B, C) Typical migration trajectories of the Zigzag-GLW and the GLW consist of two types of basic migration patterns: (D) local random searching and (E) directional persistence. The capture times Tc of the Zigzag-GLW and the GLW are shown at the lower left corner of B and C, respectively, as h:min:s. (F) Tc as functions of the target detectable radius Rt, the immunocyte density N, and the radius of the search area Ra. Tc values of the GLW were approximately 1.5-2 times larger those of the Zigzag-GLW (Tc(Zigzag-GLW) / Tc(GLW) was ~0.5-0.67). The error bars denote the SEM.
A model can be generalized to DCs' movement including dendrite motility and even neutrophils' directed migration
DCs are highly specialized for the uptake, processing, and presentation of antigens. Inherent to DC function is their ability to migrate, whereby they capture antigens in the periphery and then travel to secondary lymphoid organs to initiate immune responses by activating naïve lymphocytes [44]. The trafficking pathways of DCs have been studied in detail [44]. However, the precise search strategy of DCs for locating antigens in the periphery is less well understood since DCs are not as motile as the commonly studied T cells and neutrophils. Rather than patrolling a large area, many DCs are ideally positioned within peripheral tissues and detect danger-associated antigens by merely extending and retracting their dendrites [6, 44-46, 49-51]. In the present study, we took into account not only the actively migrating DCs but also the DCs merely extending dendrites. To include the motility information of DC dendrites, we obtained cell trajectories by tracking the cells' centroids, which changed with the extension and retraction of dendrites. Based on the DC trajectories, we studied the behavior of DCs searching for rare antigens within skin tissues. As a whole, DCs were found to execute the Zigzag-GLW search strategy. This finding indicates that the motility of dendrites is also a crucial part of the Zigzag-GLW search strategy of DCs. This unexpected strategy might help even DCs merely extending dendrites to efficiently capture antigens and initiate immune responses as soon as possible in the early stage of a disease when the antigen is still extremely rare. This might be beneficial for the immune response of various diseases ranging from infection to cancer.
Among the investigated WBCs, T cells accounted for ~31%, whereas neutrophils accounted for ~51% (Fig. S9). In general, T cells show more random walk behavior while neutrophils reveal more directed migration [6]. However, in the present study, since we used Tolfedine to relieve the inflammation caused by surgery and performed the intravital imaging at off-peak hours of inflammation response [48], the recruitment of neutrophils by directed migration was not observed. In addition, for the WBCs, trajectories superimposed after normalizing their start points to the origin (Fig. 2D) didn't show any preferred direction and the mean velocity vector, 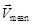 = (0.40, 0.35) μm min-1 (calculated by taking both the value and the direction of the velocity into account [23]), is approximately the size of its SEM ((0.02, 0.02) μm min-1) and nearly equal to zero. These results demonstrate that there is no directed migration for the investigated neutrophils together with T cells. Instead, the searching behavior of neutrophils was described by the random walk model, Zigzag-GLW. Nevertheless, the randomness of direction in the Zigzag-GLW model is only reflected in the general direction. Therefore, it might be possible to generalize the Zigzag-GLW model to the directed migration of neutrophils, by simply replacing the uniform general-direction distribution in the model with the distribution extracted from the directed-migration data of neutrophils.
= (0.40, 0.35) μm min-1 (calculated by taking both the value and the direction of the velocity into account [23]), is approximately the size of its SEM ((0.02, 0.02) μm min-1) and nearly equal to zero. These results demonstrate that there is no directed migration for the investigated neutrophils together with T cells. Instead, the searching behavior of neutrophils was described by the random walk model, Zigzag-GLW. Nevertheless, the randomness of direction in the Zigzag-GLW model is only reflected in the general direction. Therefore, it might be possible to generalize the Zigzag-GLW model to the directed migration of neutrophils, by simply replacing the uniform general-direction distribution in the model with the distribution extracted from the directed-migration data of neutrophils.
A series of studies have shown that immunocytes, including lymphocytes, DCs, neutrophils, microglia and others, all move forward by an amoeboid-manner crawling [1, 6, 10-13]. This behavior is recognized as a common search strategy of eukaryotic cells when the targets are out of the range of the cells' detection system [14, 15]. Combining the migration behaviors of immunocytes searching for rare targets in the native physiological environment, the Zigzag-GLW captures the essential features of the intravital crawling pattern. Thus, although this model has only been validated in the present study among DCs and WBCs consisting of mostly T cells and neutrophils, this model might be generalized to other immunocyte types as an in vivo search strategy for capturing targets out of the cells' detection ranges.
A search strategy caused by both extrinsic and inherent factors
The native physiological environment is full of closely packed cells of various types and reticular extracellular matrices. Is the Zigzag-GLW just an adaptive behavior of immunocytes, allowing them to migrate through the narrow space between cells and the extracellular matrices? Previous studies have shown that both sparsely-distributed microglia cultured in vitro (50 cells mm-2, preventing the cells from coming into contact or interacting with each other) [13] as well as lymphocytes within the complex tissue environment of the lymph node [1, 12] migrate in an amoeboid crawling pattern. However, in contrast to cells in their complex physiological environment, the zigzag-manner, directional running persists for a characteristic time frame (~10 min) and no obvious pause states are observed for sparsely-distributed cells cultured in vitro [14]. This finding indicates that the zigzag-manner, directional persistence might be an inherent movement pattern of immunocytes, whereas the different persistence times for each zigzag-manner, directional run step and the appearance of pause states might arise from an adaptation of the immunocytes' migration manner to the crowded physiological environment, responding to the frequent interactions between immunocytes and other cells or molecules. However, because the time frame of the in vivo imaging (10-20 min) is similar to the persistence time of in vitro zigzag-manner, directional running (~10 min), the validation of these inferences requires further studies.
Comparison with other classical search strategies of immunocytes
In the past decade, various mathematical models have been introduced into the field of immunology to describe the search strategy of immunocytes. Generally, only the behavior of the m.s.d. determines whether a given model is adapted to describe the experimental data. For instance, the m.s.d. as a function of time was linearly fit in standard analyses to determine whether the cell motility followed a Brownian walk [1, 12, 16, 17]. Based on the finding that the m.s.d. of T cells was not simply linearly depending on the time, but revealed rather a quadratic relation for short times and a linear relation for longer times, the Beauchemin model was proposed [19, 20]. Far more rigorous than traditional studies, by fitting the model to the migration data of T cells not only based on the behavior of the m.s.d. but also on other displacement statistics, such as P(r(t)), ζ(t), and K(τ,t), the GLW was selected from various candidate random walks to describe the search strategy of T cells [23]. Nevertheless, the GLW model assumes that a cell moves forward along a straight line during each run step and that adjacent run directions are uncorrelated. Therefore, the zigzag turning preference of immunocytes is not taken into account in the GLW model. Particularly, a crawling cell model [52] has been proven to exhibit a zigzag turning preference [13]. However, there is no evidence that this model executes a GLW-like intermittent walk like immunocytes. Moreover, the crawling cell model only incorporates the actual biochemistry and mechanics behind cell crawling [52], while it does not consider the impact of the natural physiological environment on the behavior of immunocytes.
The Zigzag-GLW model was proposed based on investigations of the in vivo searching behavior of immunocytes in their native physiological environment. The model does not only take into account the GLW-like intermittent walk but also the zigzag turning preference of immunocytes. Correspondingly, both the series of displacement statistics discussed above and several measurements on turn direction correlations and turn amplitude distribution of the model were fitted to the experimental data. In this way, we robustly demonstrated that the Zigzag-GLW model can describe the in vivo search strategy of immunocytes well.
Zigzag mode in the three-dimensional space
To analyze the zigzag mode of immunocytes in three-dimensional (x, y, z) space, four-dimensional (x, y, z, time) imaging was carried out with a z thickness of 20 μm and step size of 2 μm, to allow for capturing a z stack within 20 s. Other conditions were controlled the same as three-dimensional (x, y, time) imaging. The method used for recognizing turns was the same as that in the two-dimensional (x, y) space (Additional File 6: Fig. S2), while the process of trajectory smoothing was canceled since the time for capturing a z stack is approximately the time span of the smoothing window size (30 s). Since there are no concepts of left and right turns in three-dimensional space, we defined positive and negative turns to state the zigzag mode instead. For the ith turn in a given trajectory, a normal vector 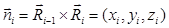 was calculated, where
was calculated, where 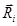 is the displacement vector directed from the ith turn point to the (i+1)th turn point. If zi > 0, the ith turn was defined positive, otherwise it was defined negative (Fig. 7A). Consequently, the turning statistics were redefined by replacing the left and right turns in them by the positive and negative turns, respectively.
is the displacement vector directed from the ith turn point to the (i+1)th turn point. If zi > 0, the ith turn was defined positive, otherwise it was defined negative (Fig. 7A). Consequently, the turning statistics were redefined by replacing the left and right turns in them by the positive and negative turns, respectively.
We found that in three-dimensional space, the zigzag turning preference still remained. Specifically, the number of data points in the second (negative-positive turns) and fourth (positive-negative turns) quadrants of the return map was obviously larger than that in the first (positive-positive turns) and third (negative-negative) quadrants (Fig. 7B), a visible anticorrelation existed between adjacent turn directions (Corr(1); Fig. 7C), and Pzigzag was obviously larger than one (the inset of Fig. 7C). Furthermore, the analyses show that the turning statistics didn't significantly change in the three-dimensional space, comparing with those in the two-dimensional space (Figs. 5D, 7B, and 7C). On the other hand, the previous study has shown that the x, y, and z components of displacements are described by the same probability density distribution [23], indicating that the analysis of displacement statistics is insensitive to the spatial dimension as well. Since both displacement statistics and turning statistics are insensitive to the spatial dimension, the whole analysis was carried out in two-dimensional space in the present study to simplify quantification and modeling.
Analysis without inactive DCs
To avoid introducing arbitrary cutoffs, we didn't exclude inactive cells from our analysis. However, in order to investigate the impact of inactive DCs on the whole analysis, we analyzed DCs excluding the immotile ones (with mean velocity Vmean < 1.2 μm min-1). In general, the whole analysis is found to be insensitive to excluding these inactive cells. On the one hand, the shapes and properties of the displacement statistics remained unchanged, while their values changed since the immotile-cell population that was excluded by a speed cutoff are, on average, slower than the full population. Specifically, the left part of the P(r(t)) corresponding to low r(t) values lost only a small amount of weight (Fig. 8A). For ζ(t) = Ctγ and m.s.d. = Atα, C increased from 0.71 to 0.88 and A increased from 2.21 to 3.11, while the values of γ and α were nearly unchanged (γ ≈ 0.62 and 0.63 for active DCs and all DCs, whereas α ≈ 1.42 and 1.44 for active DCs and all DCs, respectively). K(τ,t) was unchanged. These results are consistent with the previous study [23]. On the other hand, the turning statistics didn't significantly change as well (Fig. 8B). The result is unsurprising since a lot of inactive cells were automatically excluded in turning statistical analysis due to the limitations for turn recognition. We also performed the whole analysis on DCs excluding the ones with Vmean < 2 μm min-1. The conclusions are the same as above and the changes are magnified (data not shown).
Zigzag turning preference of leukocytes (white blood cells, WBCs) in three-dimensional (3D) space. (A) Definitions of positive and negative turns. Red dots indicate the recognized turn points (Turn), 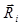 is the displacement vector directed from the ith turn point to the (i+1)th turn point in a given trajectory,
is the displacement vector directed from the ith turn point to the (i+1)th turn point in a given trajectory, 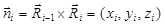 is the normal vector for the ith turn, and θ is the turn angel. The ith turn was defined positive and negative for zi > 0 and zi ≤ 0, respectively. (B) The return map of turn angles θ in 3D space. (C) The autocorrelation of turn directions Corr(k) in 3D space compared with that in two-dimensional (2D) space. k denotes the turn lag. The inset shows the comparison of the zigzag preference indexes Pzigzag. ns: no significant difference, two-tailed unpaired t test. The error bars denote the SEM. The WBC data in 3D space were obtained from three independent experiments with 1-2 mice per experiment (6 movies, 252 cells).
is the normal vector for the ith turn, and θ is the turn angel. The ith turn was defined positive and negative for zi > 0 and zi ≤ 0, respectively. (B) The return map of turn angles θ in 3D space. (C) The autocorrelation of turn directions Corr(k) in 3D space compared with that in two-dimensional (2D) space. k denotes the turn lag. The inset shows the comparison of the zigzag preference indexes Pzigzag. ns: no significant difference, two-tailed unpaired t test. The error bars denote the SEM. The WBC data in 3D space were obtained from three independent experiments with 1-2 mice per experiment (6 movies, 252 cells).
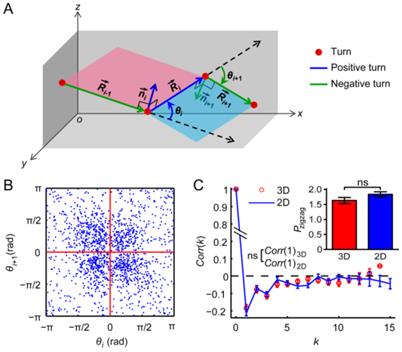
Comparison of the analysis of active dendritic cells (DCs) and all DCs. Active DCs were obtained by excluding the immotile ones (with mean velocity Vmean < 1.2 μm min-1) from all DCs. (A) Displacement probability density distributions P(r(t)) at different time intervals t. Colored dots and solid lines indicate P(r(t)) of active DCs and all DCs, respectively. The inset shows P(r(t)) of active DCs at different t after normalizing the displacement r(t) by the scale factor ζ(t) (ρ = r(t) / ζ(t)). The normalized P(r(t)) of all DCs at t = 0.17 min (solid line) and the Gaussian fitting of the normalized P(r(t)) of active DCs at t = 5 min (dashed line) are shown for comparison. (B) The autocorrelation of turn directions Corr(k) of active DCs compared with that of all DCs. k denotes the turn lag. The inset shows the comparison of zigzag preference indexes Pzigzag. ns: no significant difference, two-tailed unpaired t test. The error bars denote the SEM.
Conclusion
In conclusion, to describe the search strategy of immunocytes more accurately and comprehensively, we developed the Zigzag-GLW model, which takes the two essential features of the in vivo crawling pattern of immunocytes into account: the GLW-like intermittent walk and the zigzag turning preference. Not merely the widely concerned WBCs, also another important immunocyte type, the DCs, were found to execute the Zigzag-GLW search strategy in their native physiological environment. We demonstrated that this search strategy enables immunocytes to capture rare targets faster than GLW walkers and, accordingly, might be one of the driving factors for the efficient initiation and development of immune responses. According to the proposed model, changes in the search behavior and search efficiency of different immunocyte types could be evaluated quantitatively under various physiological and pathological conditions. Thus, combined with intravital optical imaging, the proposed model might have potential applications for the diagnosis and therapeutic-effect evaluation of diseases ranging from infection to cancer.
Supplementary Material
Additional File 1Movie S1.
Movie S2.
Movie S3.
Movie S4.
Movie S5.
Supplementary Figures, Supplementary Methods and Discussion, Supplementary Movie Legends.
Acknowledgements
We thank Dr. Zhiying He (Second Military Medical University, Shanghai, China) for presenting B6-EGFP mice. This work is supported by the National Major Scientific Research Program of China (Grant No.2011CB910401).
Abbreviations
DC: dendritic cell; GLW: generalized Lévy walk; WBC: white blood cell (leukocyte); Zigzag-GLW: zigzag generalized Lévy walk; EGFP: enhanced green fluorescent protein; AIC: Akaike information criterion; OCT: optimal cutting temperature.
Competing Interests
The authors declare no competing financial interests.
References
1. Cahalan MD, Parker I. Choreography of cell motility and interaction dynamics imaged by two-photon microscopy in lymphoid organs. Annu. Rev. Immunol. 2008;26:585-626
2. Banchereau J, Steinman RM. Dendritic cells and the control of immunity. Nature. 1998;392(6673):245-252
3. Zhou F, Li X, Song S, Acquaviva JT, Wolf RF, Howard EW. et al. Anti-tumor responses induced by laser irradiation and immunological stimulation using a mouse mammary tumor model. J. Innov. Opt. Health Sci. 2013;06(04):1350039
4. Germain RN, Robey EA, Cahalan MD. A decade of imaging cellular motility and interaction dynamics in the immune system. Science. 2012;336(6089):1676-1681
5. Alitalo K. The lymphatic vasculature in disease. Nat. Med. 2011;17(11):1371-1380
6. Weninger W, Biro M, Jain R, Leukocyte migration in the interstitial space of non-lymphoid organs. Nat. Rev. Immunol. 2014;14(4):232-246
7. Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P. Leukocyte functions and percentage breakdown. Molecular Biology of the Cell, 4th ed. New York: Garland Science. 2002
8. Nathan C. Neutrophils and immunity: challenges and opportunities. Nature Rev. Immunol. 2006;6(3):173-182
9. Kolaczkowska E, Kubes P. Neutrophil recruitment and function in health and inflammation. Nature Rev. Immunol. 2013;13(3):159-175
10. Yang TD, Kwon TG, Park J, Lee KJ. Trail networks formed by populations of immune cells. New J. Phys. 2014;16(2):023017
11. Byrne MB, Kimura Y, Kapoor A, He Y, Mattam KS, Hasan KM. et al. Oscillatory behavior of neutrophils under opposing chemoattractant gradients supports a winner-take-all mechanism. PLoS One. 2014;9(1):e85726
12. Miller MJ, Wei SH, Parker I, Cahalan MD. Two-photon imaging of lymphocyte motility and antigen response in intact lymph node. Science. 2002;296(5574):1869-1873
13. Yang TD, Park J, Choi Y, Choi W, Ko T, Kyoung J. Zigzag turning preference of freely crawling cells. PLoS One. 2011;6(6):e20255
14. Li L, Nørrelykke SF, Cox EC. Persistent cell motion in the absence of external signals: a search strategy for eukaryotic cells. PLoS One. 2008;3(5):e2093
15. Bosgraaf L, Van Haastert PJM. The ordered extension of pseudopodia by amoeboid cells in the absence of external cues. PLoS One. 2009;4(4):e5253
16. Matheu MP, Cahalan MD, Parker I. Immunoimaging: studying immune system dynamics using two-photon microscopy. Cold Spring Harb. Protoc. 2011:146-155
17. Miller MJ, Wei SH, Cahalan MD, Parker I. Autonomous T cell trafficking examined in vivo with intravital two-photon microscopy. Proc. Natl. Acad. Sci. U. S. A. 2003;100(5):2604-2609
18. Portillo IG, Campos D, Méndez V. Intermittent random walks: transport regimes and implications on search strategies. J. Stat. Mech. Theory Exp. 2011;02:P02033
19. Beauchemin C, Dixit NM, Perelson AS. Characterizing T Cell movement within lymph nodes in the absence of antigen. J. Immunol. 2007;178(9):5505-5512
20. Textor J, Sinn M, de Boer RJ. Analytical results on the Beauchemin model of lymphocyte migration. BMC Bioinformatics. 2013;14(Suppl 6):S10
21. Preston S, Waters S, Jensen O, Heaton P, Pritchard D. T-cell motility in the early stages of the immune response modeled as a random walk amongst targets. Phys. Rev. E. 2006;74(1):011910
22. Othmer HG, Dunbar SR, Alt W. Models of dispersal in biological systems. J. Math. Biol. 1988;26(3):263-298
23. Harris TH, Banigan EJ, Christian DA, Konradt C, Tait Wojno ED, Norose K. et al. Generalized Lévy walks and the role of chemokines in migration of effector CD8+ T cells. Nature. 2012;486(7404):545-8
24. James A, Plank MJ, Edwards AM. Assessing Lévy walks as models of animal foraging. J. R. Soc. Interface. 2011;8(62):1233-1247
25. Raichlen DA, Wood BM, Gordon AD, Mabulla AZP, Marlowe FW. Evidence of Lévy walk foraging patterns in human hunter-gatherers. Proc. Natl. Acad. Sci. U. S. A. 2013;111(2):728-733
26. Palyulin VV, Chechkin AV, Metzler R. Lévy flights do not always optimize random blind search for sparse targets. Proc. Natl. Acad. Sci. U. S. A. 2014;111(8):2931-2936
27. González MC, Hidalgo CA, Barabási A. Understanding individual human mobility patterns. Nature. 2008;453(7196):779-782
28. Viswanathan GM, da Luz MGE, Raposo EP, Stanley HE. The Physics of Foraging: An Introduction to Random Searches and Biological Encounters. Cambridge, UK: Cambridge University Press. 2011
29. Viswanathan GM, Buldyrev SV, Havlin S, da Luz MGE, Raposo EP, Stanley HE. Optimizing the success of random searches. Nature. 1999;401(28):911-914
30. Cannon J, Asperti-Boursin F, Fricke M, Letendre K, Moses M. T cell motility within lymph nodes fits a Lévy signature (CAM1P.225). J. Immunol. 2014;192:47.1
31. Bosgraaf L, Van Haastert PJM. Navigation of chemotactic cells by parallel signaling to pseudopod persistence and orientation. PLoS One. 2009;4(8):e6842
32. Beltman JB, Maree AFM, de Boer RJ, Spatial modelling of brief, long interactions between T cells, dendritic cells. Immunol. Cell Biol. 2007;85(4):306-314
33. Riggs T, Walts A, Perry N, Bickle L, Lynch JN, Myers A. et al. A comparison of random vs. chemotaxis-driven contacts of T cells with dendritic cells during repertoire scanning. J. Theor. Biol. 2008;250(4):732-751
34. McDonald B, Pittman K, Menezes GB, Hirota SA, Slaba I, Waterhouse CCM. et al. Intravascular danger signals guide neutrophils to sites of sterile inflammation. Science. 2010;330(6002):362-366
35. Daniels VG, Wheater PR, Burkitt HG. Functional histology: A text and colour atlas. Edinburgh, UK: Churchill Livingstone. 1979
36. Palmer GM, Fontanella AN, Shan S, Hanna G, Zhang G, Fraser CL. et al. In vivo optical molecular imaging and analysis in mice using dorsal window chamber models applied to hypoxia, vasculature and fluorescent reporters. Nat. Protoc. 2012;6(9):1355-1366
37. Sumen C, Mempel TR, Mazo IB, von Andrian UH. Intravital microscopy: visualizing immunity in context. Immunity. 2004;21(3):315-329
38. Xu J, Van Keymeulen A, Wakida NM, Carlton P, Berns MW, Bourne HR. Polarity reveals intrinsic cell chirality. Proc. Natl. Acad. Sci. U. S. A. 2007;104(22):9296-9300
39. Jacobs K. Lévy processes. Stochastic Processes for Physicists: Understanding Noisy Systems. Cambridge, UK: Cambridge University Press. 2010
40. Hannan EJ, Deistler M. Statistical theory of linear systems. Wiley series in probability and mathematical statistics. New York, USA: John Wiley and Sons. 1988:227
41. Box GEP, Jenkins GM, Reinsel GC. Time Series Analysis: Forecasting and Control, 4th ed. Hoboken, USA: Wiley. 2008
42. Hamilton JD. Time Series Analysis. Princeton, USA: Princeton University Press. 1994
43. Johnson JB, Omland KS. Model selection in ecology and evolution. Trends Ecol. Evol. 2004;19(2):101-108
44. Cavanagh LL, Weninger W. Dendritic cell behaviour in vivo: lessons learned from intravital two-photon microscopy. Immunol. Cell Biol. 2008;86(5):428-438
45. Heuze ML, Vargas P, Chabaud M, Berre ML, Liu Y, Collin O. et al. Migration of dendritic cells: physical principles, molecular mechanisms, and functional implications. Immunol. Rev. 2013;256:240-254
46. Ng LG, Hsu A, Mandell MA, Roediger B, Hoeller C, Mrass P. et al. Migratory dermal dendritic cells act as rapid sensors of protozoan parasites. PLoS Pathog. 2008;4(11):e1000222
47. Deepak AR, Le T, Bhushan V. First Aid for the USMLE Step 1 2008. New York, USA: McGraw-Hill Medical. 2007
48. Tsirogianni AK, Moutsopoulos NM, Moutsopoulos HM. Wound healing: immunological aspects. Injury. 2006;37(Suppl 1):S5-S12
49. Nishibu A, Ward BR, Jester JV, Ploegh HL, Boes M, Takashima A. Behavioral responses of epidermal Langerhans cells in situ to local pathological stimuli. J. Invest. Dermatol. 2006;126(4):787-796
50. Niess JH, Brand S, Gu X, Landsman L, Jung S, McCormick BA. et al. CX3CR1-mediated dendritic cell access to the intestinal lumen and bacterial clearance. Science. 2005;307:254-258
51. Chieppa M, Rescigno M, Huang AYC, Germain RN. Dynamic imaging of dendritic cell extension into the small bowel lumen in response to epithelial cell TLR engagement. J. Exp. Med. 2006;203(13):2841-2852
52. Satulovsky J, Lui R, Wang Y. Exploring the control circuit of cell migration by mathematical modeling. Biophys. J. 2008;94(9):3671-3683
Author contact
![]() Corresponding authors: Ling Fu and Qingming Luo. Email: lfuhust.edu.cn and qluohust.edu.cn; Phone number: (86) 27-87792033; Fax number: (86) 27- 87792034
Corresponding authors: Ling Fu and Qingming Luo. Email: lfuhust.edu.cn and qluohust.edu.cn; Phone number: (86) 27-87792033; Fax number: (86) 27- 87792034
 Global reach, higher impact
Global reach, higher impact